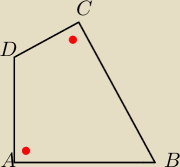
planimetria ~uczeń13: Dany jest czworokąt ABCD, w którym długości boków wynoszą: |AB|=14, |CD|=30, |AD|=48, oraz kąty DAB i BCD sa proste. długości przekątnych tego czworokąta i jego pole.

Powracający: To narysuj szkic takiego czworokata

~uczeń13:

Adamm: z tw. Pitagorasa liczysz boki, ze wzoru na pole trójkąta liczysz pole, drugą przekątną bym policzył z tw. Cosinusów

Powracający: Przekatna DB tez z tw . Pitagorasa

Adamm: mówiłem o tej drugiej

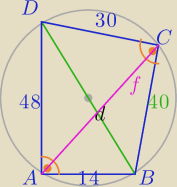
Mila: Na czworokącie ABCD można opisać okrąg (∡A+∡B=180^o) 1) d²=14²+48² d=50 |BC|=40

	1
PABCD=		*(14*48+30*40)=936
	2

2) Jeżeli czworokąt jest wpisany w okrąg to : d*f=|AB|*|DC|+|BC|*|AD| (tw.Ptolemeusza) 50*f=14*30+40*48 5f=14*3+4*48

	234
f=		=46.8
	5

Adamm: a tw. Ptolemeusza to przecież sprowadza się do tw. Cosinusów