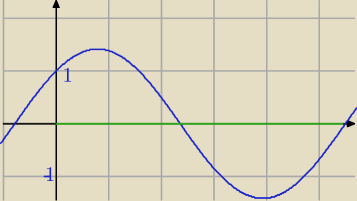
f(x)=sinx+cosx
Robert: Zbiorem wartości funkcji f(x)=sinx+cosx gdzie x ∊ <0,2π> jest:
jakim wzorem to rozgryźć?
6 kwi 17:39
Alky: Teraz już widać
sinα+sinβ=..
6 kwi 17:42
karty do gry: −√2 ≤ f(x) ≤ √2
patrz nierówność Cauchego−Schwarza
6 kwi 17:42
xd:
6 kwi 17:42
Robert: Czy mogę prosić o dalszą pomoc, bo jednak nie umiem

6 kwi 17:58
6 kwi 18:04
Janek191:
| | π | | π | | π | |
f(x) = sin x + sin ( |
| − x) = 2 sin |
| cos ( x − |
| ) = √2 cos ( x − 0,5π) |
| | 2 | | 4 | | 2 | |
więc
− 1 ≤ cos ( x −0,5π) ≤ 1 / *
√2
−
√2 ≤
√2 cos ( x − 0,5 π) ≤
√2
ZW = < −
√2,
√2 >
==================
6 kwi 18:10
Mila:
Inny sposób:
| | 1 | | 1 | |
f(x)=sinx+cosx=√2*( |
| sinx+ |
| cosx)⇔ |
| | √2 | | √2 | |
| | π | | π | |
f(x)=√2*(sinx*cos( |
| )+sin( |
| )*cosx) |
| | 4 | | 4 | |
dalej jak u
Janka
6 kwi 18:26

