Zbiór wartości adbuster33: Wyznacz zbiór wartości funkcji f (x) = ¹_{cos² x − 2 cos x − 8}

powrócony z otchłani: Poprzez analogie: https://matematykaszkolna.pl/forum/350435.html

adbuster33: Analogicznie dalej mi nie wyszło wyznaczenie wierzchołka nic mi nie daje. Proszę o pomoc

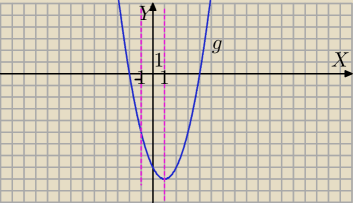
Iryt: g(x)=cos²x−2cosx−8 cosx=t i |t|≤1 g(x)=t²−2t−8=(t−1)²−1−8 g(x)=(t−1)²−9 p=1, q=−9 dla t∊<−1,1> g(x) nie ma miejsc zerowych g_min=−9 dla x=1 g_max=g(−1)=−5

	1
fmin=
	−5

	−1
fmax=
	9

	1		1
−		≤f(x)≤−
	5		9

adbuster33: Analogicznie starałem się robić kolejny podpunkt, ale tu również zgrzyt: f (x) = ⁷_{sin² − sin x − 12} sin x ∊ <−1,1> f(x) = sin² − sin x − 12 = (sin x − ¹₂)² − 12¹₄ dla sin x = −1 ⁷₁₊₁₋₁₂ = − ⁷₁₀ dla sin x = 1 − ⁷₁₂ a powinno być −⁴₇ Co jest nie tak?

adbuster33: Pomoże ktoś?

Mila: sinx=t, |t|≤1

	1
Dla g(t)=(t−		)2−1214
	2

g(t) nie ma miejsc zerowych dla t∊<−1,1>

	1
p=		∊<−1,1>
	2

	1
q=−12
	4

g_min=−12¹₄

	7
f(t)=
	1   (t− )2−1214   2

	7		4
fmax=		=−
	49   −   4		7

g_max szukamy na końcach przedziału <−1,1> g(−1)=−10 g(1)=−12 −10>−12 g_max=−10

	7
fmin=−
	10

	7		4
−		≤f(x)≤−
	10		7

adbuster33: Dzięki

Mila: