wykaż geo ana: Proszę o pomoc w dokończeniu: https://matematykaszkolna.pl/forum/350235.html

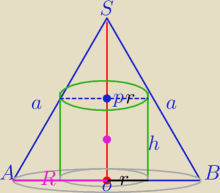
Mila: W stożek którego przekrojem jest trójkąt równoboczny wpisano walec o największej objętości. Udowodnij że objętość tego walca jest równa objętości kuli wpisanej w ten stożek.

	a√3
H=|OS|=
	2

1) Objętość kuli wpisanej w stożek:

	1		a√3
rk=		H=		− promień kuli wpisanej w ten stożek
	3		6

	4		a√3		a3√3π
Vk=		*π*(		)3=
	3		6		54

2) Walec:

|PS|		H		H−h		a√3   2		a√3   −h 2
	=		⇔		=		⇔		=r√3
r		R		r		a   2		r

	a√3
h=		−r√3
	2

	a√3
V(r)=πr2*(		−r√3)
	2

Licz V'(r)