heo anal pora: Mam romb i w nim wspolrzedne punktu S (1,1) i jest to przecięcie przekątnych. Mam też długość przekątnej, która wynosi 10.

	3		7
Prosta która zawiera ta przekątną ma wzór y= −		+
	4		4

Mam obliczyć współrzędne bokow (leżą one na tej prostej)

Antonni: Popraw rownanie prostej Przekatne w rombie sie polowia i przecinaja pod kątem prostym

pora:

	3		7
y = −		x +
	4		4

i jak to mam ugryźć?

Kasia: https://matematykaszkolna.pl/forum/349138.html

Kasia: Najlepiej "dziadkiem do orzechów" !

pora: ?

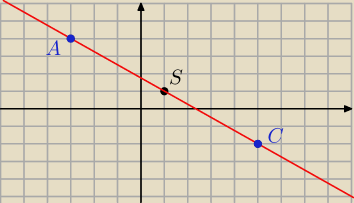
Antonni: Z warunkow zadania masz ze AC=10 Czyli wiemy ze przeatne sie polowia wiec AS= SC=5

	3
Skoro punkt A nalezy do prostej AC to znaczy ze bedzie mial wspolrzedne (x, −		x+
	3

	7
		)
	4

ze wzoru na odleglosc dwoch punktow (czyli punktu S od punktu A ) wylicz wspolrzedne punktu A Potem z ewzoru na srodek odcinka wylicz wspolrzedne punktu C Albo chyba prosciej mozna wyznaczyc wspolrzedne tych punktow Napiszmy rownanie okregu o srodku S i promieniu r=5 (x−1)²+(y−1)²=25 Masz rownanie prostej AC woec policz punkty przecia sie prostej z okregiem Z warunku zadania te punty wlasnie masz policzyc

adam: A(−3,4), C(5,−2) Ale w zadaniu jest "obliczyć współrzędne bokow (leżą one na tej prostej)", czyli należącej do przekątnej. Co prawda oblicza się współrzędne wierzchołków, ale nic nie stoi na przeszkodzie, by boki leżały na prostej należącej do przekątnej. Otrzymamy wtedy rąb o drugiej przekątnej równej 0 i polu też równym 0. Obliczmy wierzchołki B i D takiego rąbu. Zwróćmy uwagę, że możemy otrzymać dwa rąby o wierzchołkach ABCD oraz AB'CD' Długość boku to a=√10 Więc potrzebne są dwa równania okręgów o środkach A i C, i r=a. (x + 3)² + (y − 4)² = 10 (x − 5)² + (y + 2)² = 10 Przecinając prostą leżącą na przekątnej z tymi okręgami otrzymamy: B(−3 − 4√2/5, 4 + 3√2/5), D(5 − 4√2/5, 3√2/5 − 2) B'(4√2/5 − 3, 4 − 3√2/5), D'(5 + 4√2/5, −2 − 3√2/5) P.S. Powyższe to oczywiście tylko zabawa.

kochanus_niepospolitus: adam ... jak sobie wyobrażasz, że BOK rombu leżał na tej samej prostej co przekątna rombu? Aby wyznaczyć punkty B i D należy wyznaczyć prostą m ⊥ do prostej którą masz podaną w zadaniu ... na tej prostej będą leżeć punkty B i D |AB| = |CB| = |AD| = |CD| i wyznaczasz (całą rodzinę) punktów B i D ... chyba że masz jeszcze jakiś warunek, którego nie podałeś PS. rĄbu rĄbu PS.2 Romb o 'przekątnej równej 0' Że co