geometria analityczna Tomaszek:

	700
Punkt A(23,22) jest wierzchołkiem trójkąta prostokątnego o polu		. Prosta AC zawiera
	3

przeciwprostokątną tego trójkąta, a prosta zawierająca przyprostokątną AB ma równanie 3y−4x+26=0.Środek okręgu wpisanego w trójkąt ABC ma współrzędne S=(−2,−3).Oblicz współrzędne wierzchołków B i C wyszło mi B(−1,−10) i C mi nie wyszedł. 1)Napisałem równanie okręgu wpisanego w trójkąt 2)policzyłem punkt P(2,−6) leżący na boku AB 3)|AP|+r=35+5=40

	4		26
4)policzyłem współrzędne wierzchołka B(x,		x−		) ze wzoru
	3		3

	70
5)Obliczyłem długość 2 boku ze wzoru na pole P=1/2*a*b b=
	6

6)napisałem prostą prostopadłą do AB przechodzącą przez punkt B

	3		43
7)nie mogłem policzyć wierzchołka C(x,−		x−		) z tego samego wzoru z punktu 4)
	4		4

Tomaszek: up

Tadeusz: Przecież współrzędne punktu B możesz wyznaczyć

Tomaszek: no to wyznaczyłem i wyszło mi B(−1,−10) , a jak mam B to i mam C, ale nie mogę tego dobrze policzyć

adam: C(−31/3,−3) B(−1,−10) A(23,22) i wszytko się zgadza. Podpowiem, że przyprostokątna BC to: y = −(3 x)/4 − 43/4

adam: Upss, raczej chodziło mi o przeciwprostokątną, że to: y = (3 x)/4 + 19/4

Tomaszek: jak policzyłeś prostą przeciwprostokątną?

adam: Ze stycznej do okręgu przechodzącej przez A

Tomaszek: rozumiem, ale nie wiem jak Ci to wyszło.

adam: https://matematykaszkolna.pl/forum/152643.html

Tomaszek:

	4		26
ja zrobiłem to tak y=		x−
	3		3

podstawiłem to do równania (x+2)²+(y+3)²=25 doszedłem do (x−2)²=0 x=2 i y=−6

Tomaszek: B(−1,−10) mi wyszło potem napisałem prostą prostopadłą przechodzącą przez punkt B(−1,−10)

	3x		43
i wyszło y=−		−
	4		4

	70
Policzyłem z Pola długość boku BC=
	6

i jest to odległość punktu B od C

4900		−3x		43
	=(x+1)2+(		−		+10)2
36		4		4

Tomaszek: to wie ktoś co robię źle?

adam: BC zgadza się: 35/3.

adam: To teraz rozwiąż układ równań: {prosta BC {okrąg S=B r=35/3

Tomaszek: no właśnie jakieś dziwne liczby mi wychodzą

	1225		9		18		9
x2+2x+1−		+		x2+		x+		=0
	9		16		16		16

25		50		1225		9
	x2+		x−		+1+		=0
16		16		9		16

Δ=202500+1937500 √Δ=1462,87

adam: {y=−(3x)/4−43/4 {(x + 1)² + (y + 10)² = 1225/9 i musi wyjść. Oczywiście wyjdą dwa rozwiązania, ale tylko jedno jest właściwe, te z większym y.

Mila: A ile ma wyjść C ?

Tomaszek: C(−31/3,−3) tyle napisał adam, ja nie mam dostępu do odpowiedzi.

adam: C(−31/3,−3)

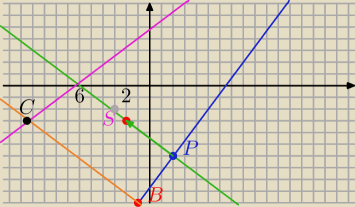
Mila: 1) k: −4x+3y+26=0

	|−4*(−2)+3*(−3)+26
d(S,k)=		=5
	√42+32

2) prosta SP: 3x+4y+C=0 i S∊prostej⇔C=18 3x+4y+18=0 P− Punkt przecięcia prostych 3x+4y+18=0 i −4x+3y+26=0 P=(2,−6) SP^→=[4,−3] u→⊥SP^→ u^→=[3,4] lub [−3,−4] 3) P=(2,−6)→T_[−3,−4]→B=(−1,−10) 4) Prosta BC: 3x+4y+C=0 i B∊prostej⇔C=43 3x+4y+43=0

	35
5) |AB|=40, |BC|=
	3

BC^→=k*PS^→=[−4k,3k]

	35
√16k2+9k2=
	3

	7
k=
	3

	28
BC→=[−		,7]
	3

6)

	31
B(−1,−10)→T[−28/3,7]→=C=(−		,−3)
	3

===================================

Tomaszek: dziękuję

Mila: