współśrodkowe okręgi nowy: Dane są dwa współśrodkowe okręgi. W mniejszym okręgu ( o promieniu r) zaznaczono średnicę, na większym okręgu ( o promieniu R) wybrano punkt P. Wykaż, że suma |PA|² + |PB|² jest stała (tzn. nie należy od wyboru punktu P na większym okręgu). Rozważ dwa przypadki.

'Leszek: Co to sa punkty A i B , srednica malego okregu ?

nowy: Tak (zapomniałem to napisać )

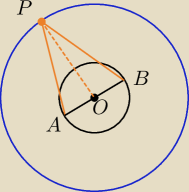
kochanus_niepospolitus: Dla przypadku I (patrz rysunek ... uwaga −−− PO nie jest prostopadłe do AB) |PO| = R |AO| = r |PA| = √R² + r² − 2rR*cos(∡POA) |PB| = √R² + r² − 2rR*cos(∡POB) Należy zauważyć, że ∡POB = 180 − ∡POA ... czyli cos(∡POB) = − cos(∡POA) A więc: |PA|² + |PB|² = 2R² + 2r² = const. (bo nie zależy od kąta ∡POA) Dla przypadku II −−− AO współliniowa z PO |PA| = R − r |PB| = R + r A więc: |PA|² + |PB|² = R² − 2Rr + r² + R² + 2Rr + r² = 2R² + 2r² = to samo co wcześniej c.n.w.

kochanus_niepospolitus: Jedyne co trza było wykorzystać w zadaniu to: 1) Tw. cosinusów: https://matematykaszkolna.pl/strona/543.html 2) Wzory redukcyjne funkcji trygonometrycznych: https://matematykaszkolna.pl/strona/430.html

ElizaR: Można prościej, na płaszczyźnie Gaussa: niech z=0 będzie środkiem obu okręgów. równanie dużego |z| = R, małego |z|=r. Jeśli AB jest średnicą małego, to A(a) i B(−a) (w nawiasie afiksy obydwu punktów). Niech z będzie dowolnym punktem dużego okręgu.Tworzymy sumę ____ ____ |z−a|² + |z+a|² = (z−a)(z−a) + (z+a)(z+a) = (po wymnożeniu i redukcji) = 2(R² =r²). _ ( pamiętamy, że x*x =|x|²) Dlaczego wyrzucono liczby zespolone z programu szkolnego?

kochanus_niepospolitus: Liczby zespolone z programu szkolnego wywalono bardzo dawno temu (już za czasów 'starej matury' ich nie było)

piotrek: