Objętość graniastosłupa prawidłowego trójkątnego
Lasrew: W graniastosłupie prawidłowym trójkątnym krawędź podstawy ma długość a. Przekątna ściany
bocznej tworzy z drugą ściana boczną kąt alfa. Wyznacz objętość graniastosłupa.
Prawidłowa odpowiedź to
| a3 √3(3 − 4 sin2 alfa) | |
| |
| 8 sin alfa | |
Proszę o dokładne rozwiązanie.
4 mar 15:11
4 mar 15:38
fiodor21: teoretycznie podobne, ale tam są konkretne dane, ponadto jest podany trójkąt 30,60,90, gdzie
mając daną długość jednego boku możemy policzyć pozostałe.
licząc moje zadanie tym sposobem mnożą mi się tylko kolejne niewiadome
4 mar 16:25
Mila:
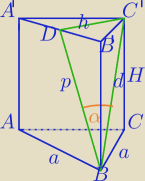
2) W ΔC'DB:
3) W ΔC'CB:
| | a√3 | |
d2=a2+H2⇔H2=( |
| )2−a2 |
| | 2 sinα | |
| | a2*3 | | 3 | |
H2= |
| −a2, H2=a2*( |
| −1) |
| | 4sin2α | | 4sin2α | |
4)
| | a2√3 | | √3−4sin2α | |
V= |
| *a* |
| |
| | 4 | | 2 sinα | |
| | a3*√3*(3−4sin2α) | |
V= |
| |
| | 8sinα | |
==================
4 mar 22:33
'Leszek: Dobrze byloby jeszcze rozwazyc problem dla jakich wartosci kata α zadanie ma
rozwiazanie , a mianowicie wyrazenie 3 − 4 sin2α > 0 ⇒ α = ( 0 , π/3 )
4 mar 22:56
