ttt tade: Zerknie ktoś? Nie mam odpowiedzi do zadania, sprawdzi ktoś czy jest dobrze? Wyznacz wszystkie wartosci parametru m, dla których dwa różne pierwiastki równania są wieksze od 1 (m+1)x²−3mx+4m=0 zdjęcie: http://imgur.com/a/yqCSz

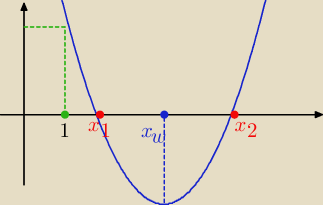
5-latek: Warunki Δ>0 af(1)>0 x_w>1

Eta: 1/ a≠0 2/ Δ>0 3/ f(1)>0 4/ x_w>1

tade: zrobiłem takie warunki ale dla m+1>0 czyli ramion skierowanych w góre przedziały sie nie pokrywały ale dla m+1<0 i x_w>1 oraz f(1)<0 coś mi tam wyszło

Eta: 1/ m+1≠0 ( nie jest ważne czy parabola ramionami do góry czy do dołu)

tade: tak, m≠−1 bo bedzie rownanie liniowe, spróbuje jeszcze raz te warunki moze jakis błąd sie wkradł

5-latek: https://matematykaszkolna.pl/forum/347321.html Tutaj sie o to pytam

5-latek: Powinienes dodstac odpowiedz

	16
−		<m<−1
	7

Robilem to samo zadanie z tym ze u mnie bylo delta ≥0 (nie bylo slowa roznych

tade:

	−1
jesli f(1)=m+1−3m+4m=2m+1>0 to m>		co z poprzednimi warunkami w ogóle sie nie pokrywa
	2

czy coś źle licze? Eta czemu bierzesz pod uwage tylko gdy ramiona są skierowane w góre przecież przy x² jest m+1 wiec jesli m<−1 to chyba wtedy wyjdzie?