zadanka PrzyszlyMakler: 1.Narysuj w układzie współrzędnych figurę będącą zbiorem punktów, których współrzędne x,y spełniają układ nierówności x² +y²−6|y|≤9. Oblicz pole tej figury. Doszedłem do tego, że to są okręgu o wzorach x² + (y−3)² ≤18 x² + (y+3)² ≤18 i potrafię sobię wyobrazić/narysować tę figurę, ale nie wiem jak obliczyć ten fragment pola, gdy te oba okręgi na siebie nachodzą, aby go odjąć. 2.Dla jakich wartości parametru a iloczy różnych miejsc zerowych funkcji f określonej wzorem f(x)=log₃²x − (a²−a)log₃x +1−a jest równy 9 Wiadomo, zmienna t, Δ>0 ale w rozwiązaniu zmieniają warunek x₁*x{2}=9 na x₁+x₂ = 2 domyślam się, że pewnie chodzi o to, że dodając logarytmy one się mnożą, ale nie potrafię tego wyprowadzić i dokładnie zrozumieć samemu, więc bardzo proszę o rozpisanie i komentarz.

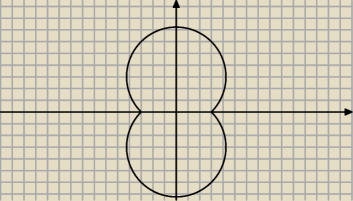
Adamm: x²+y²−6|y|≤9 ⇔ x²+(|y|−3)²≤18 dla y≥0 mamy koło x²+(y−3)²≤18 dla y<0 mamy koło x²+(y+3)²≤18 a tak to właśnie wygląda

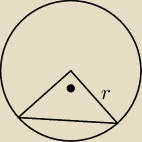
Adamm: oblicz pole wycinka, pole trójkąta

PrzyszlyMakler: Dzięki Adamm, już wszystko jasne. A pomoże ktoś z zadaniem 2?

PrzyszlyMakler: Czy ktoś mógłby spróbować to zadanie drugie?

relaa: 345301.

PrzyszlyMakler: Dziękuję relaa. Kosmos to zadanie..