Dwa wierzchołki trójkąta ABC maja współrzędne A(2,1) B(1,4). Punkt C na osi OY
Rockuu:
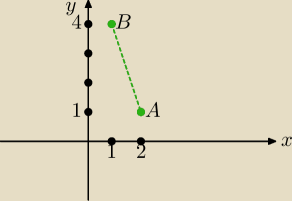
Dwa wierzchołki trójkąta ABC maja współrzędne A(2,1) B(1,4). Punkt C znajduje sie na osi OY.
Wyznacz wszystkie możliwe położenie punktu C, tak aby trójkąt ABC był prostokątny.
Punkt C oznaczam jako C(0,m)
generalnie opcje są trzy:
1) kąt prosty jest przy C
2) przy A
3) albo przy B
I tutaj jest pytanie czy pierwsza opcja jest na pewno możliwa bo licząc z twierdzenia
pitagorasa
|BC|
2+|AC|
2=|AB|
2
po podstawieniu 1
2+(4−m)
2+2
2+(1−m)
2=2
2
po uproszczeniu m
2−5m+9=0 => Δ<0
Z tego wynika, że nie ma takiej opcji aby przy C był kąt prosty, czy może coś źle liczę albo w
ogóle
nie tak to sie robi?
24 lut 14:44
Jerzy:
A jaka jest długość odcinka AB ?
24 lut 14:51
Rockuu: ... Dobra już widze swój błąd √12+32=√1+9=√10
nie podniosłem 3 do kwadratu i wyszło mi √4
24 lut 14:57
Rockuu: Dziękuje
24 lut 14:58
Jerzy:
Najprościej rozwiazać to wektorami.
24 lut 14:59
Rockuu: w sumie to racja, nawet nie pomyślałem o tym
24 lut 15:00
24 lut 15:27
 Dwa wierzchołki trójkąta ABC maja współrzędne A(2,1) B(1,4). Punkt C znajduje sie na osi OY.
Wyznacz wszystkie możliwe położenie punktu C, tak aby trójkąt ABC był prostokątny.
Punkt C oznaczam jako C(0,m)
generalnie opcje są trzy:
1) kąt prosty jest przy C
2) przy A
3) albo przy B
I tutaj jest pytanie czy pierwsza opcja jest na pewno możliwa bo licząc z twierdzenia
pitagorasa
|BC|2+|AC|2=|AB|2
po podstawieniu 12+(4−m)2+22+(1−m)2=22
po uproszczeniu m2−5m+9=0 => Δ<0
Z tego wynika, że nie ma takiej opcji aby przy C był kąt prosty, czy może coś źle liczę albo w
ogóle
nie tak to sie robi?
Dwa wierzchołki trójkąta ABC maja współrzędne A(2,1) B(1,4). Punkt C znajduje sie na osi OY.
Wyznacz wszystkie możliwe położenie punktu C, tak aby trójkąt ABC był prostokątny.
Punkt C oznaczam jako C(0,m)
generalnie opcje są trzy:
1) kąt prosty jest przy C
2) przy A
3) albo przy B
I tutaj jest pytanie czy pierwsza opcja jest na pewno możliwa bo licząc z twierdzenia
pitagorasa
|BC|2+|AC|2=|AB|2
po podstawieniu 12+(4−m)2+22+(1−m)2=22
po uproszczeniu m2−5m+9=0 => Δ<0
Z tego wynika, że nie ma takiej opcji aby przy C był kąt prosty, czy może coś źle liczę albo w
ogóle
nie tak to sie robi?