zadania jkjhj: zd28 Dwa wierzchołki trójkąta ABC mają współrzędne A(2,1),B(1,4).Punkt C znajduje się na osi OY.Wyznacz wszystkie możliwe położenie punktu C takie że trójkąt ABC jest trójkątem prostokątnym. zd27 W sześcianie o krawędzi 6 odcięto naroża prowadząc płaszczyzny wyznaczone przez środki krawędzi o wspólnym wierzchołku..Wyznacz pole powierzchni i objętość pozostałej bryły.

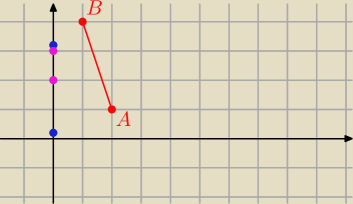
cosinusx: C leży na osi OY=> C(0,c) 1) AB jest jedną z przyprostokątnych równanie prostej przechodzącej przez A i B y=a₁x+b₁ 1=2a₁+b₁ 4=1a₁+b₁ −3=a₁ b₁=7 y=−3x+7 a₁=−3, więc druga przyprostokątna (która musi być do niej prostopadła) musi mieć współczynnik kierunkowy taki, że −3*a₂=−1

	1
Zatem a2=
	3

Dodatkowo druga przyprostokątna musi przechodzić przez punkt A lub B. 1.1 Druga przyprostokątna przechodzi przez A

	1
y=		x+b2
	3

A(2,1)

	1
1=		*2+b2
	3

	1
b2=
	3

	1
y=U{1}[3}x+
	3

I ta prosta ma też przechodzić przez C:

	1
c=U{1}[3}*0+
	3

	1
c=
	3

	1
Zatem C ma współrzędne C(0,		)
	3

1.2 Druga przyprostokątna przechodzi przez B

	1
y=		x+b3
	3

B(1,4)

	1
4=		*1+b3
	3

	1
b3=3
	3

	1
y=U{1}[3}x+3
	3

I ta prosta ma też przechodzić przez C:

	1
c=U{1}[3}*0+3
	3

	1
c=3
	3

	1
Zatem C ma współrzędne C(0,3		)
	3

2) AB jest przeciwprostokątną Zatem prosta zawierająca punkty C i A jest prostopadła do prostej zwierającej C i B Prosta przechodząca przez A(2,1) i C(0,c) y=a₄x+b₄ 1=2a₄+b₄ c=0a₄+b₄ b₄=c 2a₄=1−b₄

	1−c
a4=
	2

Prosta przechodząca przez B(1,4) i C(0,c) y=a₅x+b₅ 4=1a₅+b₅ c=0a₅+b₅ c=b₅ a₅=4−c A ponieważ są prostopadłe, to zachodzi a₄*a₅= −1

1−c
	*(4−c)=−1
2

(1−c)(4−c)=−2 4−c−4c+c²=−2 c²−5c+6=0 Δ=25−24=1 c₁=2 c₂=3 Zatem C(0,2) lub C(03,)

	1		1
Odp. C może mieć następujące współrzędne: C(0,2), C(0,3), C(0,		), C(0,3		)
	3		3

Eta: Można prościej ( z wykorzystaniem wektorów ) Jeżeli trójkąt ABC ma być prostopadły, to: → → → → → → CA ⊥CB lub CA⊥AB lub CB⊥AB z treści zadania : A(2,1), B(1,4) , C(0,y) z warunku prostopadłości wektorów mamy ( pomijam strzałki nad wektorami dla łatwości zapisu) CA=[2,1−y] i CB=[1,4−y] ⇒ 2*1+(1−y)(4−y)=0 ⇒ y²−5y+6=0 ⇒(y−2)(y−3)=0 ⇒y=2v y=3 C₁(0,2), C₂(0,3)

	1
CA=[2,1−y] i AB=[1,−3] ⇒ 2−3+3y=0 ⇒ y=
	3

C₃(0,1/3)

	11
CB=[1,4−y] i AB=[1,−3] ⇒ 1−12+3y=0 ⇒ y=
	3

C₄(0,11/3

Eta: 2 sposób Wystarczy skorzystać z warunku prostopadłości prostych wyznaczyć współczynniki kierunkowe( bez wyznaczania równań prostych) Jeżeli proste AC⊥BC to a_AC *a_BC= −1

	1−y		4−y
aAC=		, aBC=
	2		1

to (1−y)(4−y}= −2 ⇒ ........... y=2 v y=3 i podobnie lub a_AC*a_AB= −1 lub a_BC*a_AB=−1 ..........................