Trójkąt równoboczny w geometrii analitycznej. Smerf: W trójkąt równoboczny o wierzchołku C(3, −5) wpisano okrąg o środku S(−1, −3). Wyznacz współrzędne wierzchołków A oraz B.Wyliczyłem A(−3−√3;−2−2√3) B(−3+√3;−2+2√3) Mógłby ktoś sprawdzić?

Mila:

1
	*CS→=SD→
2

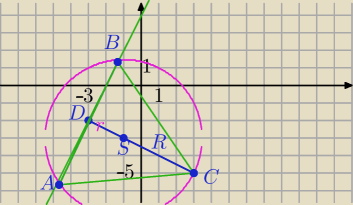
CS^→=[−4,2] S=(−1,−3)→T{[−2,1]⇒D=(−1−2,−3+1)=(−3,−2) Prosta SC: C(3, −5) −3=−a+b −5=3a+b −−−−−−−−− odejmuję stronami

	1
2=−4a, a=−		, b=−3.5
	2

	1
y=−		x −3.5
	2

Prosta AB: y=2x+b i D∊prostej, −2=−6+b, b=4 y=2x+4 3) Punkty A i B − punkty przecięcia prostej AB i okręgu o środku S i R=√4²+2²=√20 (x+1)²+(y+3)²=20 (x+1)²+(2x+4+3)²=20 x=−3−√3 lub x=−3+√3 y=−2−2√3 lub y=−2+2√3 A=(−3−√3 ,−2−2√3) , B=(−3+√3 ,−2+2√3)

Smerf: ostatni krok liczyłem trochę inaczej, ale wyniki się zgadzają więc nie jest źle. Dzięki po raz drugi dzisiaj

Mila: Pewnie liczyłeś długość boku Δ.

Mila: Miło pomagać komuś, kto tym się interesuje. Są osoby , które wrzucają zadania na forum , za 2 lub 3 dni zadają pytanie : a dlaczego tak?.

Smerf: Tak obliczyłem długość boku W poniedziałek sprawdzian z planimetrii i geometrii analitycznej i się przygotowuję

Mila: Powodzenia. Widzę, że dobry poziom wiedzy prezentujesz.

5-latek: Dobry wieczor Milu Lub tak https://matematykaszkolna.pl/forum/306447.html

Smerf: Staram się sam rozwiązywać zadania i jak mam odpowiedzi wynik się zgadza to super, ale czasami tak mnie zamula że nie mogę czegoś dopatrzeć albo źle odejmę i zadanie nie wychodzi i dopiero wtedy sprawdzam na Internecie a nie jak niektórzy co nie chce im się rozwiązywać i szukają gotowca

Mila: Tak trzymać!

Mila: Z jakiego zbioru korzystasz?

Smerf: Zostało mi ostatnie. Miałabyś jakąś wskazówkę? Wyliczyłem długość AD i nie wiem jak wykorzystać to do wyliczenie promienia którego mi tylko brakuje a zadanie jest takie:Z punktu P(−1,0) poprowadzono sieczną i styczną do okręgu o środku w punkcie S(1,√6) sieczna jest odległa od środka okręgu o 1 i przecina go w punktach B oraz D. Punkt A jest punktem wspólnym okręgu i stycznej. Wiedząc że odcinek AB jest średnicą okręgu wyznacz równanie okręgu.

Smerf: Na lekcjach ze zbioru Pazdry a te zadanie przygotował nam specjalnie nauczyciel

Mila: Zaraz, tylko zrobię rysunek.

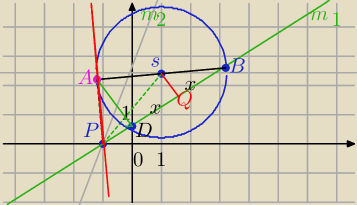
Mila: P=(−1,0) S=(1,√6) |PS|=√2²+√6²=√10 Z punktu P można poprowadzić dwie styczne do okręgu i sieczne m− jedna z siecznych odległa o 1 od pktu S m: y=ax+b , 0=−a+b, b=a m: y=ax+a, ax−y+a=0

	|a*1−√6+a|
d(S,m)=		=1
	√a2+1

stąd

	2√6−3		2√6+3
a=		lub a=
	3		3

	2√6−3		2√6−3		2√6+3		2√6+3
m: y=		*x+		lub y=		*x+
	3		3		3		3

Q − środek cięciwy |DB|=2x D∊Okręgu ⇒r²=x²+1², r²=x²+1 |PS|²=1²+|PQ|²⇔10=1+|PQ|² |PQ|=3 A − punkt styczności stycznej s i okręgu. Z tw. o odcinkach stycznej i siecznej: |PA|²=|PD|*(|PD|+2x) |PA|²=(3−x)*(3+x) |PA|²=9−x² D∊okręgu, AB jest średnicą AD||QS |AD|=2 WΔADP: |AP|²=2²+|PD|² Dalej poradzisz sobie. Do jutra. DObranoc

Smerf: Nie musiałaś rozpisywać całego zadania. Myślałem nad tymi warunkami z tw. Pitagorasa i tw. o stycznej i siecznej, ale miałem za dużo niewiadomych bo nie dostrzegłem, że obliczyć odcinek PQ Dzięki wielkie