pochodna
Info: Obliczyć pochodną lewostronną f(x)=x−2|x| w punkcie x=0
15 lut 23:09
XL: dla Δx < 0 przyrost funkcji Δy w punkcie x = 0
− wynosi:
Δy = 0+Δx +2(0+Δx) = 3Δx
| | Δy | |
czyli f'(x) = lim(Δx→0−) |
| = 3 |
| | Δx | |
16 lut 10:18
Info: a jeśli mamy f(0−)=|x| to będzie f(0−)=|0+|
16 lut 10:33
XL:
po prostu 0
16 lut 10:36
16 lut 10:37
16 lut 10:40
Info: f(0+h)=h−2|h|
a tamto to f'(0)=−1
16 lut 10:41
Jerzy:
Nie mieszaj:
f(x) = x − 2IxI
| | f(0+h) − f(0) | | h − 2IhI − 0 | | IhI | |
f'(0−) = limh→0− |
| = limh→0− |
| = 1 − 2 |
| |
| | h | | h | | h | |
= 1 + 2h = 3
16 lut 10:47
Jerzy:
@XL
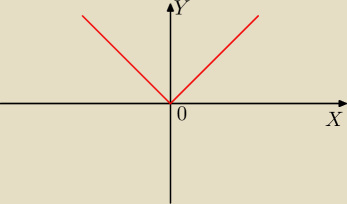
Dla funkcji: f(x) = IxI :
− pochodna lewostronna = − 1
− pochodna prawostronna = 1
16 lut 10:48
Info: IhI przy lim h→0
− to 0
− 
16 lut 10:53
Jerzy:
limh→0−|h| = limh→0−(−h) = 0
16 lut 11:01
Info: thx
16 lut 11:04
XL: @Jerzy przecież chodziło o pochodną
17 lut 09:19
Jerzy:
OK. Myślałem,że napisałeś ,że pochodna f(x) = |xI jest równa 0
17 lut 09:26