ttt tade: kiedy suma dwóch wyrażen ma wartość stałą? potrzebne do zadania

5-latek: napisz zadanie

tade: uzasadnij, że dla każdej liczby x∊(−1;5) wyrażenie √4x²+12x+9+2√x²−12x+36 ma wartość stałą narazie to tylko wyciągnełem z pod pierwiastkow (2x+3)+2(x+6)

5-latek: jesli juz to |2x+3| i 2|x+6| √x²= |x|

tade:

	a		b		a2+b2
może coś takiego zastosować a+b =		+		=		jakies pomysły?
	b		a		ab

5-latek: Poprawka oczywiscie 2|x−6|

tade: ale jestli x∊(−1;5) to mozna zdjac wartosc bezwzgledna i bedzie 2x+3+2(−x+6)=2x+3−2x+12=3+12=15 o i samo wyszło

5-latek: teraz |2x+3|+2|x−6|=|2x+3|+|2x−12| Teraz |2x+3| dla tego [rzedzialu =2x+3| |2x−12| dla tego przedzalu = −(2x−12)= −2x+12= 12−2x 2x+3+12−2x=

5-latek: I gitara

tade: po algebrze ostatnie zadanie przed spaniem dowód geometryczny, jakos niemoge go rozgryźć a pewnie jest łatwy, no nic dzieki

5-latek: Pisz tem dowod Mnie sie tez przyda ,

5-latek: https://matematykaszkolna.pl/forum/344723.html zobacz tez na to zadanie

tade: Dany jest trójkąt ABC w którym BC = a. Z wierzchołka B poprowadzono środkową BD do boku AC. Punkt S jest środkiem odcinka BD. Przez punkty A i S poprowadzono prostą, która przecieła bok

	2
BC w punkcie P. Wykaż, że długosc odcinka CP jest rowna		a
	3

Postawiłem sobie za cel rozwiązac to zadanie bez pomocy wiec narazie nie prosze o takową. Zerkne tez na zadanie które wysłałeś moze cos mi wpadnie do głowy

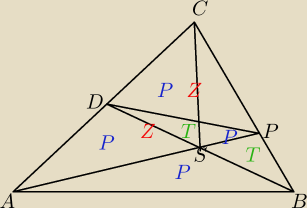
tade: Udało się W trójkącie ADP: Z=P+T W trójkącie BCD: 2T+Z=2P podstawiam 2T+P+T=2P 3T=P

	1		2
T=		P ⇒ trójkąt CPS =		P, mają taką sama wysokość wiec CP jest dwa razy dluższy od
	3		3

PB