Trojkat prostokatny
5-latek:
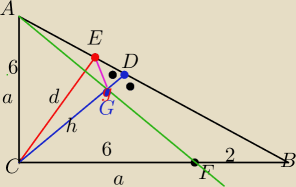
Co do tego zadania nalezy powtorzyc?
Zadanie :
W trojkacie prostokatnym o przyprostokatnych BC=a=8 i AZ=b=6 wyprowadzono z wierzcholka C
wysokosc CD i
dwusieczna CE oraz odmierzono na boku BC odcinek CF=b=6
Prosta AF przecina wysokosc CD w punkcie G
Obliczyc dlugosc odcinka EG
Zrobilem rysunek do zadania zeby wiedziec gdzie bedzie wysokosc a gdzie dwusieczna
2 lut 23:19
Ajtek:
I na rysunku jest pomylona wysokość z dwusieczną. Witaj
5−latek 
.
2 lut 23:22
5-latek:
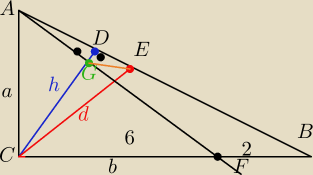
Czesc
Ajtek
Ajjjj Nie w tym miejscu przylozylem cyrkiel
Wiec muszse go poprawic. Teraz powinno byc dobrze
2 lut 23:31
5-latek: Zauwazylem tylko ze ΔACF to Δ prostokatny rownoramienny i wtedy wysokosc sie pokryje z
dwusieczna (ale co mnie to da ?
2 lut 23:38
Ajtek:
Może się przydać twierdzenie o dwusiecznej, to raz. Szukaj Δ podobnych, prostokątnych.
2 lut 23:44
5-latek: Znalazlem takie
ΔACD≈ΔDCB na podsatwie cechy KKK
2 lut 23:50
Ajtek:
h masz znane, d masz znane, AD i BD również, co za tym idzie ED też, teraz myślimy co dalej.
2 lut 23:58
5-latek: Wyskosc h moge policzyc bo P
ABC=8*6*0,5= 24
| | 24 | |
i PABC= 0,5*10*h= 24 to 5h=24 to h= |
| |
| | 5 | |
3 lut 00:00
5-latek: Nie wiem jak obliczyc AD i BD
Wiem tylko ze beda to odcinki na jakie wysokosc podzielila przeciwprostokatna wiec nalezy
zastosowac tw ze
h= √AD*BD
3 lut 00:04
Ajtek:
małolatek AD masz z Δ prostokątnego, BD również.
3 lut 00:09
5-latek: Dobra . Z pitagorasa oblicze AD
BD= 10−3,6= 6,4
3 lut 00:11
Ajtek:
To DE masz znane. Teraz sprawdź czy Δ DGE jest podobny do Δ−tów ADC i BCD. Jeśli tak, to masz
rozwiązane zadanko.
3 lut 00:14
Ajtek:
Aha, nie sprawdzam obliczeń
3 lut 00:15
5-latek: Ajtek chyba pozno (Ile wynosi DE?
3 lut 00:16
Ajtek:
Nie wiem, nie liczę. Tylko głośno myślę nad tym co widzę.
3 lut 00:19
Ajtek:
Nawet nie wiem czy w dobrą stronę idziemy
.
3 lut 00:19
5-latek: Nie potrafie tego zadania dokonczyc
Jeszcze te podobienstwa u mnie leza . Wiec jesli mozesz to proszse skoncz
3 lut 00:20
5-latek: Napiszse odpowiedz do zadania
3 lut 00:21
5-latek: Oblczenia sa dobre (pierwiastek robilem na kalkulatorze
3 lut 00:22
Ajtek:
5−latku, jutro, po pracy, po korepetycjach, około 21−szej się nad tym pochylę. Teraz
znikam spać, do roboty rano. Spokojnej
3 lut 00:27
5-latek: Dobranoc
Ajtek
Na razie dzieki . Jeszcze chwile tez posiedze
3 lut 00:29
5-latek: A jesli by tak
Kat AFB ma miare 135
o
Jesli FB jest rowniolegle do FB to wtedy ΔAGE ≈AFB
Bo jesli jest rownolegle to kat AGE= 135
o
Wtedy byn mogl ulozyc proporcje
3 lut 00:53
5-latek: Eta
Jesli spojrzysz to zadanie nr 1 z czesci 2 (geomettria i trygonomrtia Kartasinski OKolowicz
3 lut 01:00
Eta:
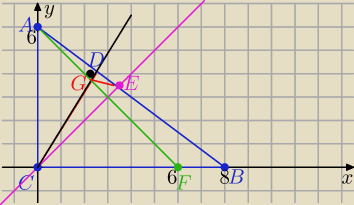
Wykorzystuję "narzędzia" geometrii analitycznej
C(0,0) , A(0,6) , B(8,0), F(6,0)
Piszę równania prostych:
| | −3 | | 4 | |
AB: y= |
| x +6 , CD : y= |
| x , CE: y=x , AF: y= −x+6 |
| | 4 | | 3 | |
Wyznaczam współrzędne punktów E i G
| | 24 | | 24 | |
CE∩AB={E} ⇒ .... E( |
| , |
| ) |
| | 7 | | 7 | |
| | 18 | | 24 | |
i AF∩ CD={G} ⇒ ...... G( |
| , ( |
| ) |
| | 7 | | 7 | |
| | 6 | | 6 | |
teraz już ............... |GE|2= ...... =( |
| )2 ⇒ |GE|= |
| |
| | 7 | | 7 | |
Miłych snów
3 lut 01:39
5-latek: Dziekuje i dobranoc
Rowniez zycze miłych snow
)
3 lut 01:42
Eta:
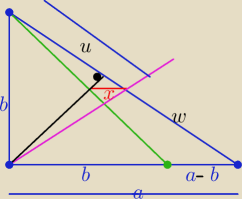
Nie mogę zasnąć
...... to podaję 2 sposób
| a−b | | w | | a | | w | |
| = |
| +1 i z tw. o dwusiecznej : |
| = |
| |
| x | | u | | b | | u | |
| | a−b | | a | | a−b | | a+b | |
to |
| = |
| +1 ⇒ |
| = |
| ⇒ |
| | x | | b | | x | | b | |
| | (a−b)*b | | 2*6 | | 6 | |
x= |
| = |
| = |
| |
| | a+b | | 14 | | 7 | |
3 lut 03:26
KKrzysiek: @Eta, to wszystko przez tę sesję! Rozumiem Cię, ja też uczę się do egzaminu.
3 lut 03:32
Eta:
3 lut 11:44
5-latek: dzien dobry
Ta sesja Cie wykonczy
3 lut 12:01
Ajtek:
WItam, widzę, że ktoś miał problemy ze snem, a taka miałem nadzieję, że powalczę sobie z
zadankiem
.
3 lut 20:32
5-latek: Witaj
Ale w sumie krotko rozwalila to zadanie ?
3 lut 20:37
Ajtek:
Eta nie lubi się guzdrać
.
3 lut 20:47
5-latek: To jest bardzo stary zbior zadan (1966r) Ajtek
3 lut 20:50
Ajtek:
Ło, to bardzo fajny zbiorek
3 lut 20:56