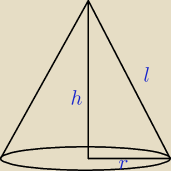
 Wyznacz pole powierzchni kuli wpisanej w stożek, którego przekrojem osiowym jest trójkąt
równoramienny o polu S i największym kącie równym 120.
Wyznacz pole powierzchni kuli wpisanej w stożek, którego przekrojem osiowym jest trójkąt
równoramienny o polu S i największym kącie równym 120.
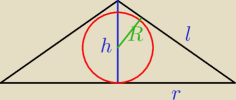 sin60 = R/(h−R)
h=l*cos60
l=√2S/sin60
sin60 = R/(h−R)
h=l*cos60
l=√2S/sin60

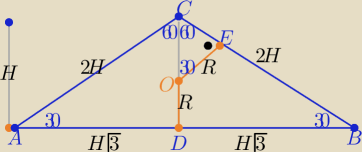
| S√3 | ||
P(ABC)=H*H√3 = S ⇒ H2= | ||
| 3 |
| |AC| | |OC| | 2H | H−R | ||||
= | ⇒ | = | ⇒ 2R=√3H−√3R | ||||
| |AD| | |OE| | H√3 | R |
| √3H | 3H2 | √3S | ||||
⇒ R= | /2 ⇒ R2= | podstaw za H2= | ||||
| 2−√3 | (2+√3)2 | 3 |
 Pewnie nie rozumie "tw. o dwusiecznej"
Pewnie nie rozumie "tw. o dwusiecznej" 
 Tak, nie napisałam tam jakiego kąta dotyczy ta dwusieczna.
Tak, nie napisałam tam jakiego kąta dotyczy ta dwusieczna.

| a+b+c | 4H+2H√3 | |||
S= R*p p= | = | = H(2+√3) | ||
| 2 | 2 |
| S | 1 | S | ||||
R= | i S= | |AB|*|CD| ⇒S= H2√3 ⇒ H2= | ||||
| H(2+√3) | 2 | 2√3 |
| S2 | ||
R2= | =............. dokończ | |
| H2(2+√3)2 |
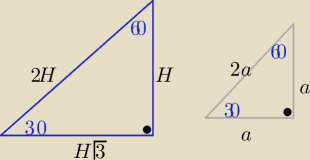 trójkąt ekierka z gimnazjum ...
trójkąt ekierka z gimnazjum ... 