zadanie

zadanie Blue: Oblicz objętość kuli wpisanej w czworościan foremny o krawędzi a. emotka

13 gru 11:14

Tadeusz: ... zrób dobry rysunek i wszystko będzie jasne − emotka

13 gru 11:20

Blue: Jeszcze z tym mam problem Krawędź podstawy ostrosłupa prawidłowego trójkątnego ma długość a, a krawędź boczna 2a. Wyznacz promień kuli wpisanej w ten ostrosłup.

13 gru 11:23

Blue: https://matematykaszkolna.pl/forum/36896.html − znalazłam to, ale tutaj wynik wyszedł inny niż w odpowiedziach..

13 gru 11:25

Tadeusz: ... a jaka jest odpowiedź w tym pierwszym? πa³/24

13 gru 11:47

Tadeusz: ... bardzo ładnie. Wrzucić ... i niech się inni zajmują Twoimi zadaniami ... Ty wpadniesz później... BYE

13 gru 12:12

Blue:

	√6
nieee, jest		πa³, Tadeusz nie obrażaj się
	216

13 gru 14:08

Blue: Po pierwsze Tadeusz, to Ty też nie odpowiedziałeś od razu, a po drugie, przecież lepiej nie tracić czasu na czekanie i robić coś pożytecznego w tym czasie, przecież ja Ci też nie każę odpowiadać od razu emotka

To tak na usprawiedliwienie, ale się nie obrażaj emotka

13 gru 14:26

Tadeusz: ... Twoja sprawa ... nie moja. Nie obrażam się ... ale mnie już na Twoich postach nie ma.

13 gru 14:33

Blue: Dlaczego?

13 gru 18:06

Lukas: Bo jak ktoś chcę Ci pomóc to poświęca swój czas a Ty go olewasz.. Dlatego...

13 gru 18:07

Mila: Zadanie. Krawędź podstawy ostrosłupa prawidłowego trójkątnego ma długość a, a krawędź boczna 2a. Wyznacz promień kuli wpisanej w ten ostrosłup. Napisz odpowiedź.

13 gru 19:29

Blue:

	(3√5−1)√33
Mila, odpowiedź:		a
	132

13 gru 21:37

Blue: Lukas, wcale nie olewam emotka

Po prostu czasem nie zaglądam od razu, ale zawsze odpowiadam ...

13 gru 21:38

Mila: Tak mam, czy to zrobiłaś w końcu?

13 gru 21:39

Blue: Szczerze, to nawet drugi raz do tego nie zajrzałam, bo robiłam maturkę . emotka

13 gru 21:58

Blue: jutro spróbuję to ruszyć, a jak nic nie wymyślę, to się do Ciebie zwrócę. O ile będziesz miała czas mi pomóc oczywiście emotka

13 gru 21:59

Mila: To podpowiem.

13 gru 22:13

Mila:

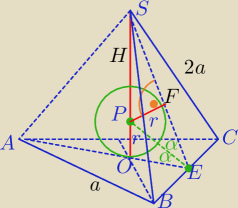
1) Kula jest styczna do ścian, punkty styczności leżą na wysokościach ścian bocznych. 2) Środek kuli (P) leży na wysokości ostrosłupa i na dwusiecznej kąta SEA. 3) z tw. o dwusiecznej w ΔOES:

r		H−r
	=
\|OE\|		\|SE\|

SF,H, OE łatwo obliczysz.

13 gru 22:16

Blue: Mila, czy ten promień w pierwszym zadaniu (to na samej górze, które wrzuciłam) powinien wyjść

	a√11

	12+2√3

14 gru 11:49

Blue:

	a√2
pomyłka r=
	4√3

14 gru 15:05

Blue: Teraz mi dobrze wyszło emotka

14 gru 15:05

Blue: To drugie też mi wyszło emotka

Dziękuję za podpowiedź emotka

14 gru 15:25

Mila:

	a√6
1) r=		− promień kuli wpisanej w czworościan foremny o krawędzi a.
	12

	a√6
2) R=		− promień sfery opisanej na czworościanie foremnym o krawędzi a.
	4

14 gru 15:46

Blue: Mila, mam jeszcze problem z tym : Wyznacz pole powierzchni kuli wpisanej w stożek, którego przekrojem osiowym jest trójkąt równoramienny o polu S i największym kącie równym 120.

	2a+a√3
Liczę to ze wzoru S= pr, gdzie p=		, mogę to tak liczyć Bo mi coś źle wynik
	2

wychodzi, ale nie wiem, czy ze względu na błędy rachunkowe, czy coś źle liczę po prostu... i a

	4√3s
= √
	3

14 gru 16:03

Blue: Wyszło mi emotka

Ale obliczenia nieprzyjemne... emotka

14 gru 16:29

Mila: Możesz tak liczyc. Tworząca to a? Jaka odpowiedź?

14 gru 16:30

Mila: Mam obliczenia dość proste.

14 gru 16:34

Blue: tak, tworząca emotka

Odp. P= 4πS(7√3−12) emotka

14 gru 16:57

Mila:

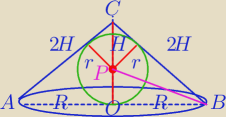
	R
sin60^o=
	2H

√3		R
	=
2		2H

R=√3H

	1
S=		2RH
	2

√3H²=S⇔

	S
H²=		( Nie licz H )
	√3

Z tw. o dwusiecznej

r		H−r		√3*H
	=		⇔r=
R		2H		2+√3

P_k=4π*r² P_k=4π*(7√3−12)*S

14 gru 17:07

Blue: no to ja to inaczej liczyłam emotka

14 gru 23:10