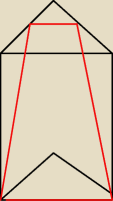
Oblicz cosinus kąta, jaki płaszczyzna przekroju tworzy z dolną podstawą granias Andrzej: Graniastosłup prawidłowy trójkątny przecięto płaszczyzną przechodzącą przez krawędź dolnej podstawy i środki dwóch krawędzi górnej podstawy. Otrzymany przekrój ma pole równe a2. Oblicz cosinus kąta, jaki płaszczyzna przekroju tworzy z dolną podstawą graniastosłupa. Proszę o pomoc i objaśnienie rozwiązania. Rozwiązanie z https://matematykaszkolna.pl/forum/320102.html nie satysfakcjonuje mnie. Pozdrawiam

Jack: tu nie ma nic co by bylo nie jasne...

Andrzej: Rozumiem Pana "wyrozumiałość", ale byłbym wdzięczny mimo wszystko za wprowadzenie jakiejkolwiek symboliki choćby z rozwiązania podlinkowanego i wyjaśnienie co z czego się bierze, gdyż geometria nie należy do mojej dziedziny i po prostu nie mogę sobie wyobrazić tego.

Jack:

	1
1. Liczymy pole tego przekroju ze wzoru na trapez (P =		(a+b) * h),
	2

gdzie a to krawedz podstawy, h to wysokosc trapezu. Wiemy, ze ta plaszczyzna przechodzi przez " środki dwóch krawędzi górnej podstawy"

	1
a to oznacza, ze gorna podstawa trapezu =		dolnej (gdyz w podstawie mamy trojkat
	2

rownoboczny)

	1
Oznaczamy dolna krawedz podstawy jako "a". Wtedy gorna =		a
	2

	1		1
zatem pole trapezu (czyli tej plaszczyzny) − ze wzoru =		* (a +		a) * h
	2		2

Z polecenia wiemy, ze pole tej plaszczyzny = a², zatem przyrownujemy je do siebie

1		1
	* (a +		a) * h = a2 /*2
2		2

3
	a * h = 2a2 / * 2
2

3ah = 4a² / : a (mozemy podzielic, bo podstawa na pewno nie ma dlugosci zero) 3h = 4a

	4
h =		a
	3

	x
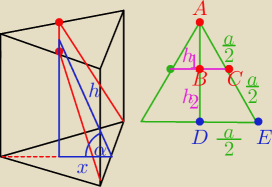
No i liczymy cosinus. Na moim rysunku to jest cos α =
	h

h − > znamy potrzebujemy jeszcze x. Jak go znalezc ? Patrz zielony trojkat na rysunku. Wiemy, ze dokladnie na srodku krawedzi jest ta plaszczyzna. wiec potrzebujemy znalezc "h₂" (do cosinusa)

	a√3
h1 + h2 to wysokosc trojkata rownobocznego czyli
	2

z Podobienstwa trojkatow ABC i ADE (z cechy kat−kat−kat)

|AB|		|AD|
	=
|AC|		|AE|

h1		a√3   2
	=
a   2		a

	a2√3
a * h1 =		(wynika to z mnozenia "na skos") teraz dzielimy przez a
	4

	a√3
h1 =
	4

My potrzebujemy h₂ , a nie h₁, zatem

	a√3		a√3		a√3		a√3
h2 =		− h1 =		−		=
	2		2		4		4

Teraz juz wszystko mamy, gdyz

x

h1

a√3   4

a√3

3

3√3

cos α =

=

=

=

*

=

h

h

4   a   3

4

4a

16

(Z tym fragmentem to faktycznie kolega skrocil)

Andrzej: Dziękuję ślicznie, właśnie nie byłem pewny co do kąta oraz skąd wzięło się h1. Teraz wszystko jasne. Pozdrawiam i jeszcze raz dziękuję.

Mila: https://matematykaszkolna.pl/forum/340782.html

Jack: chociaz z drugiej strony... skoro to sa srodki krawedzi trojkata rownobocznego

	1		a√3		a√3
to polowa wysokosci to jest		*		=
	2		2		4

to chyba nie potrzebnie liczylem.