planimetria
Rafal: Czytając wczorajsze zadanie z planimetrii, przekręciłem nieco jego treść, przez co
rozwiązywałem (właściwie, próbowałem rozwiązać) zadanie o następującej treści:
W trójkącie równoramiennym ABC ramiona AC i BC mają długość a, a promień okręgu wpisanego w ten
trójkąt ma długość r. Oblicz pole trójkąta ABC.
Może się mylę, ale zastosowane tam sztuczki w tym przypadku nie działają. A zatem, jak je
zrobić?
31 gru 18:30
Jack:
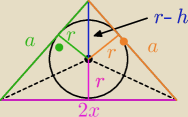
robilem wczoraj bardzo podobne zadanie...
| | 1 | |
Pole trojkata = |
| * 2x * h = x * h |
| | 2 | |
pole tego trojkata mozemy wyrazic rowniez poprzez pole tych 3 trojkatow, gdzie r jest
wysokoscia,
a bok jest podstawa, czyli
| | 1 | | 1 | | 1 | | 1 | |
P = |
| r * a + |
| r * a + |
| r * 2x = |
| r(a+a+2x) = r(a+x) |
| | 2 | | 2 | | 2 | | 2 | |
zatem
x*h = r(a+x)
no i z Pitagorasa
h
2 = a
2 − x
2 (byc moze sie przyda, ze a
2−x
2 = (a−x)(a+x))
mamy 2 rownania
{xh = r(a+x)
{h
2=a
2−x
2
rozwiaz.
31 gru 19:27
Jack: tam oczywiscie h − r a nie r − h.
31 gru 19:28
31 gru 19:32
Rafal: Jack, właśnie problem tkwi w tym, że tego układu nie da się rozwiązać zwykłym
podstawieniem, ale może pokombinuje z tym wzorem skróconego mnożenia.
31 gru 19:45
Rafal: up
3 maj 18:48
3 maj 19:29
Rafal: Dzięki
Zerknę, ale chyba nie dzisiaj
3 maj 19:36