Zależności w trójkącie równoramiennym Załamana: W trójkącie równoramiennym ABC, w którym |AB|=|BC|, wpisano okrąg. Oblicz pole tego trójkąta, jeśli |AB|=2a i promień okręgu wpisanego ma długość r.

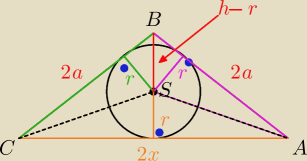
Jack: Pole trojkata to suma pol 3 malych trojkatow. Oznaczmy S jako srodek okregu, wtedy mamy :

	1
Pole trojkata BSC =		* 2a * r = ar
	2

	1
Pole trojkata BSA =		* 2a * r = ar
	2

	1
Pole trojkata CSA =		* 2x * r = xr = ? (oznaczylismy podstawe jako 2x dla uproszczenia
	2

rachunkow) Niech h oznacza wysokosc trojkata, wtedy z pitagorasa : h² = (2a)² − x² h² = 4a² − x² brakuje mi jakies drugie rownanie... Na pewno dobre dane podane?

Załamana: Tak dane się zgadzają. Zadanie ze sprawdzianu w drugiej liceum, poziom rozszerzony.

Jack: jesli zadnego kata nie ma podanego no to przy tych danych zadanie jest nie do rozwiazania. (chyba ze naprawde czegos tu nie widze)

Załamana: Zrobiłam błąd przepisując treść. Miało być |BC|=|AC|. Przepraszam... Podstawa jest 2a.

Jack: czyli |AC| = |BC| oraz |AB| = 2a?

Załamana: Tak

Jack: nadal mamy za duzo niewiadomych : D

Jack: albo nie, chwilka

Załamana: Czekam bo sama straciłam nadzieję

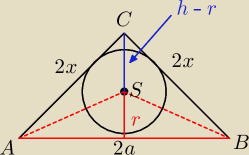
Jack: zatem Pole ABC = P_ΔABS + P_ΔBSC + P_ΔCAS

	1
PΔABS =		* 2a * r = ar
	2

jako ze rownoramienny to P_ΔBSC = P_ΔCAS

	1
PΔBSC =		* 2x * r = xr = PΔCAS
	2

zatem P_ΔABC = ar + 2xr z Pitagorasa h² = (2x)² − a² h² = 4x² − a²

	a2+h2		√a2+h2
x2 =		−−−>> x =
	4		2

podstawiajac do wzoru na pole :

	√a2+h2
PΔABC = ar + 2r *
	2

P = ar + r√a²+h²

	1
wiemy, ze pole to : PΔABC =		* 2a * h = ah
	2

(ze zwyklego wzoru ) porownujemy. ar + r√a²+h² = ah r√a²+h² = ah − ar r√a²+h² = a(h−r) /² (moge podniesc do kwadratu bo bez watpienia h > r ) r²(a²+h²) = a²(h²−2hr+r²) a²r² + r²h² = a²h² − 2a²hr + a²r² a²h² − 2a²hr − r²h² = 0 /:h (moge bo wysokosc jest wieksza od zera) a²h − 2a²r − r²h = 0 h(a² − r²) = 2a²r

	2a2r
h =
	a2−r2

no i mamy w koncu h. Zatem ostatecznie :

	1		2a2r
Pole =		* 2a * h = a*h = a *
	2		a2−r2

Jesli cos skopalem to przepraszam, ale powinno byc git.

Jack: troche zagmatwalem ale ogolnie chodzi o to, aby pole wyrazic za pomoca "a" i "r" Zadanie takie na 3 etapy.

	1
(1) wiemy ze pole trojkata =		* podstawa * wysokosc
	2

ale nie znamy wysokosci wiec musimy ja jakos wyrazic przez "a" i "r" korzystamy zatem z innego wzoru na pole, a mianowicie, (2) Pole trojkata (w ktore jest wpisany okrag) to pole 3 trojkatow zatem

	1
P =		* r * obwod
	2

(3) Porownujemy pola by znalezc nasza wysokosc i ostatecznie wyrazic pole poprzez zmienne ktore nam dali

Załamana: Dziękuję bardzo

Mila: Mój wynik (trochę inna metoda) jest taki sam. Myślę, że jest łatwiejszy sposób na to (trudne ) zadanie.

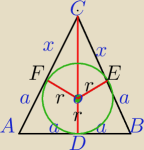
Mila: W trójkącie równoramiennym ABC, w którym |AC|=|BC|, wpisano okrąg. Oblicz pole tego trójkąta, jeśli |AB|=2a i promień okręgu wpisanego ma długość r. |DB|=|BE|=a 1)

	2a+2a+2x
PΔ=		*r=(2a+x)*r
	2

	1
PΔABC=		*2a*h=a*h
	2

(1) a*h=(2a+x)*r 2)

	x		h
ΔCOE∼ΔCDB⇔		=		stąd:
	r		a

	x*a
h=
	r

	x*a2
3) Podstawiam do (1)⇔		=(2a+x)*r⇔x*a2=r2*(2a+x)
	r

x*a²=2a*r²+x*r² x*a²−x*r²=2a*r²

	2a*r2
x=
	a2−r2

	2a*r2		r2		a2−r2+r2
PΔ=r*(2a+		)=2a*r*(1+		)=2a*r*(
	a2−r2		a2−r2		a2−r2

	a2
PΔ=2a*r*
	a2−r2

	2a3*r
PΔ=
	a2−r2

============

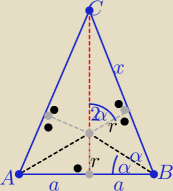
Eta: P(ABC)= 2ar+rx

	r		2tgα		2ar
tgα=		tg(2α)=		=......=
	a		1−tg2α		a2−r2

	2ar2
x=r*tg(2α)=
	a2−r2

	2ar3		2a3r
P(ABC)= 2ar+		=
	a2−r2		a2−r2

Mila: Witaj poświątecznie Eto. Właśnie o tym mówiłam, ale przeglądam książkę i nie wiem jak zaawansowani są z trygonometrią. Chodzi mi o wzór na tg(2α).

Eta: Witaj Milu Wzór na tg(2α) jest w karcie wzorów maturalnych

Mila: Tak, wiem, ale to uczennica drugiej klasy. Dobranoc