W trójkącie ABC punkt D leży na boku AB w taki sposób, że AD=2 i BD=3. matematyka moja pasja: W trójkącie ABC punkt D leży na boku AB w taki sposób, że AD=2 i BD=3. Punkt E i F leży odpowiednio na bokach BC i AC. Wiedząc, że [ABC]=10 i pole trójkąta ABE jest równe polu czworokąta DBEF, wyznacz pole trójkąta ABE.

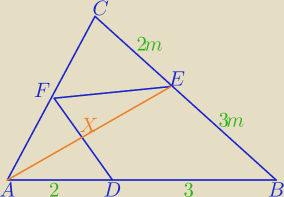
Rafal: Niech X będzie punktem przecięcia prostych AE i DF. Z równości [ABE]=[DBEF] wynika, że [ADX]=[EFX], a w szczególności [ADE]=[DEF]. Ponieważ trójkąty ADE i DEF mają wspólną podstawę DE, więc wysokości opuszczone z wierzchołków A i F na prostą DE są jednakowej długości. Oznacza to, że DE||AF, czyli też DE||AC.Z twierdzenia Talesa istnieje takie m, że |CE|=2m i |EB|=3m. Rysując wysokości (na rysunku nie miałem już miejsca) łatwo zauważyć z podobieństwa trójkątów prostokątnych, że wysokość opuszczona z wierzchołka E na prostą AB do wysokości opuszczonej z wierzchołka C na tę samą prostą ma się jak 3:5, a zatem [ABE] : [ABC]=3:5, co implikuje [ABE]=6.

Kacper:

Mila:

tomek:

Rafal: Cieszę się, że profesjonalistom się podoba, szczególnie że w temacie https://matematykaszkolna.pl/forum/340496.html ostro skłamałem. Mam nadzieję, że ktoś mnie poprawi

Kacper: Ja to sobie bardziej zaznaczam jako ciekawe zadanko, a nie patrzę na rozwiązanie. Twoje pomysły są bardzo ciekawe

Mila: Ja zauważam piękne rozwiązanie