Wyznacz stosunek u{BM}{MC}, matematyka moja pasja: ABCD jest czworokątem wypukłym. Wyznacz stosunek ^BM_MC, jeśli punkt M jest w taki sposób położony na boku BC, że odcinek AM dzieli czworokąt na dwie figury o równych polach.

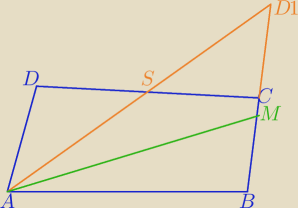
Rafal: Niech S będzie środkiem odcinka CD. Niech D' będzie odbiciem symetrycznym punktu A względem punktu S. Czworokąt ACD'D to równoległobok (bo jego przekątne przecinają się w połowie), a zatem [ASD]=[CSD'], w szczególności [AMCD]=[AMD']. Równość [ABM]=[AMCD]=[AMD'] zachodzi wtedy i tylko wtedy, gdy |BM|=|MC|+|CD'|=|MC|+|AD|. (*) Jednocześnie |BM|+|MC|=|BC| (**). Podejrzewam, że łącząc te dwie równości i rozwiązując prosty układ równań, wyznaczymy |BM| i |MC| w zależności od |BC| i |AD| − to zakończy zadanie.

Kacper:

Rafal: Właśnie się zorientowałem, że to rozumowanie działa tylko, gdy ABCD jest trapezem. Sama idea wydaje mi się dobra, ale wymaga zmodyfikowania. Może Mila coś wymyśli.

matematyka moja pasja: Czy ktoś mi pomoże ?

Kacper: Zadania na konkurs?

matematyka moja pasja: dokładnie

Kacper: No to trzeba samemu.