aaa
PrzyszlyMakler:
Witam,
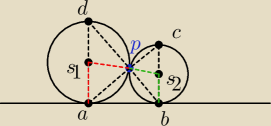
Dwa okręgi są styczne zewnętrznie w punkcie P. Poprowadzono prostą, styczną do obu okręgów
odpowiednio w punktach A i B Wykaż, że kąt ∡APB jest prost.
Czy mogłem to zrobić w ten sposób? :
Kąt CPB jest oparty na średnicy, więc jest prosty. Trójkąt PS
2B jest równoramienny, więc
kąty o wierzchołkach p i b mają równe miary− α.
Trójkąt PS
1A jest równoramienny, więc kąty o wierzchołkach P i A mają równe miar− β
Kąty CPS
2 i S
1PA są wierzchołkowe, tak samo jak kąty DPS
1 i BPS{2}. Więc kąt prosty
PCB składa się z kątów α+β= 90
Kąt półpełny na prostej S
1PS
2 zawiera kąt α + APB + β= 180
więc APB = 90
C.N.U
1) Czy by uznano taki sposób rozwiązania?
2) Mam wątpliwości czy trzeba udowodniać, że APC to prosta współliniowa, a jeżeli trzeba, to
jak to zrobić?
19 gru 16:12
PrzyszlyMakler: Więc kąt prosty
PCB składa się z kątów α+β= 90
***
tam miało być CPB
19 gru 16:14
PrzyszlyMakler: f5
19 gru 17:31
5-latek: Na jakiej pofdstawie stwerdziles ze trojkat AS1P jest rownoramienny (bo jest
19 gru 17:38
Adamm: 5−latek, punkt S1 jest środkiem okręgu, punkty A, P leżą na tym okręgu,
ponieważ okrąg to zbiór punktów równo odległych środka okręgu to |AS1|=|PS1|
19 gru 17:43
5-latek: Czesc

19 gru 17:44
Adamm: cześć
19 gru 17:45
PrzyszlyMakler: Stwierdzilem tak, bo w ramionach ma promienie

. A ktos powie czy dobrze?
19 gru 18:05
Mila:
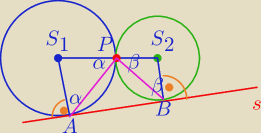
I sposób
ΔAPS
1,ΔBPS
2− trójkąty równoramienne
s− wspólna styczna
Czworokąt ABS
2S
1− trapez ⇔
Suma miar kątów przy ramieniu jest równa 180
o.
∡S
1+∡s
2=180⇔
180−2α+180−2β=180⇔
180=2α+2β
α+β=90
o⇔
|∡APB|=90
o
II sposób za chwilę.
19 gru 18:13
Mila:
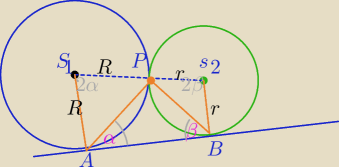
II
Kąt między styczną a cięciwą jest równy kątowi wpisanemu opartemu na tej cięciwie,
a odpowiadający kąt środkowy jest dwa razy większy.
2α+2β=180
⇔α+β=90
o⇔
|∡APC|=90
0
19 gru 18:23
19 gru 18:28
PrzyszlyMakler: Milu, a czy możesz ocenić moje rozwiązanie? I jak można udowodnić, że APC(mój rysunek) są
współliniowe?
19 gru 18:36
5-latek: probowal bym tak
U siebie na rysunku masz DAII BC jako prostopadle do stycznej
Wiec ABCD to trapez prostokatny
MOze jak zrobisz inny rysunek to kaze sie ze ten czworokat to trapez rownoramienny
19 gru 19:14
Adamm: skoro kąt APB jest równy 90o, a kąt BPC jako kąt wpisany wynosi 90o, to chyba nie ma
wątpliwości że A, P, i C są współliniowe
19 gru 19:20
Adamm: ok, teraz widzę że w swoim dowodzie PrzyszlyMakler użył tego że A, P oraz C są
współliniowe
19 gru 19:23
Mila:
Dowód dobry, może zbyt przegadany.
Możesz narysować prostopadłą do AB przechodzącą przez punkt P i wykazać , że APC=180o.
19 gru 20:17
Mila:
Makler, jeżeli ja mam jakieś wątpliwości, to szukam innego rozwiązania.
Masz dużo wiadomości i trzeba wyszukać (w głowie) te, które najprościej pozwolą rozwiązać
problem.
Ty często idziesz w zaparte tą samą ścieżką, chociaż okazuje się, że jest wyboista.
19 gru 20:20
PrzyszlyMakler: Wiem, ale nie moja wina, że wpadłem na taki pomysł a nie inny ; ) wydawał mi się dobry. P.S
Dziękuje Milu
19 gru 20:53
PrzyszlyMakler: Co do drugiego sposobu chcę się upewnić 2α+ 2β= 180
równość 180 wzięłaś oczywiście z kątów w trapiezie czy z czegoś innego?
19 gru 21:03
Mila:
Tak w trapezie, ale już nie objaśniałam, bo było w I sposobie.
19 gru 21:14
PrzyszlyMakler: Oki, dziękuję Milu, zawsze miałem problem ze zrouzmieniem tego drugiego twierdzenia. To było b
sprytne go użycie.

Te okręgi mi nie podeszły.. Ale juz na szczescie koncze planimetrię...
Nie mogę się doczekać aż się zabiorę za arkusze

19 gru 21:16
Mila:
Powodzenia.

19 gru 21:17
Metis: Makler do kiedy można składać deklaracje? Nic sie nie zmieniło?
19 gru 21:20
Mila:
Metis, jak na studiach? Dużo masz matematyki? Jakoś nie wpisujesz tu zadań.
19 gru 21:26
Metis: Dobry wieczór
Milu 
Wybór
Wrocławia 
był najlepszą decyzją.
Z matematyką jestem na biężąco, pierwsze kolokwium z analizy dopiero po świetach, więc przez
ten okres będę działał

Algebra to na razie same podstawy − kończymy macierze.
Mam świetnych wykładowców, na razie nie mogę narzekać.
Gorzej z poznawaniem nowych osób − to zdecydowanie na
minus.
Pozdrawiam

19 gru 21:35
PrzyszlyMakler: @Metis, bodajże do 7 lutego, ja już złożyłem dawno

. Tak, została mi końcówka planimetrii,
analityczna, stereo, prawdopodobieństwo i pochodne. Myślę, że od lutego już wezmę arkusze w
dłoń

. Działam, Ty też będziesz poprawiać?
19 gru 21:43
Mila:
To miło czytać takie komentarze. Powodzenia
Metis, pracuj pilnie.

Jak pewnie wiesz, jestem fanką matematyków wrocławskich.
19 gru 21:55
Metis:
Milu tak czytałem już o tym kiedyś na forum
 Makler
Makler Podejdę sobie do matematyki, ale tylko dla własnej satysfakcji(albo i niesaty...

)
19 gru 22:08
 Witam,
Dwa okręgi są styczne zewnętrznie w punkcie P. Poprowadzono prostą, styczną do obu okręgów
odpowiednio w punktach A i B Wykaż, że kąt ∡APB jest prost.
Czy mogłem to zrobić w ten sposób? :
Kąt CPB jest oparty na średnicy, więc jest prosty. Trójkąt PS2B jest równoramienny, więc
kąty o wierzchołkach p i b mają równe miary− α.
Trójkąt PS1A jest równoramienny, więc kąty o wierzchołkach P i A mają równe miar− β
Kąty CPS2 i S1PA są wierzchołkowe, tak samo jak kąty DPS1 i BPS{2}. Więc kąt prosty
PCB składa się z kątów α+β= 90
Kąt półpełny na prostej S1PS2 zawiera kąt α + APB + β= 180
więc APB = 90
C.N.U
1) Czy by uznano taki sposób rozwiązania?
2) Mam wątpliwości czy trzeba udowodniać, że APC to prosta współliniowa, a jeżeli trzeba, to
jak to zrobić?
Witam,
Dwa okręgi są styczne zewnętrznie w punkcie P. Poprowadzono prostą, styczną do obu okręgów
odpowiednio w punktach A i B Wykaż, że kąt ∡APB jest prost.
Czy mogłem to zrobić w ten sposób? :
Kąt CPB jest oparty na średnicy, więc jest prosty. Trójkąt PS2B jest równoramienny, więc
kąty o wierzchołkach p i b mają równe miary− α.
Trójkąt PS1A jest równoramienny, więc kąty o wierzchołkach P i A mają równe miar− β
Kąty CPS2 i S1PA są wierzchołkowe, tak samo jak kąty DPS1 i BPS{2}. Więc kąt prosty
PCB składa się z kątów α+β= 90
Kąt półpełny na prostej S1PS2 zawiera kąt α + APB + β= 180
więc APB = 90
C.N.U
1) Czy by uznano taki sposób rozwiązania?
2) Mam wątpliwości czy trzeba udowodniać, że APC to prosta współliniowa, a jeżeli trzeba, to
jak to zrobić?

 . A ktos powie czy dobrze?
. A ktos powie czy dobrze?
 I sposób
ΔAPS1,ΔBPS2− trójkąty równoramienne
s− wspólna styczna
Czworokąt ABS2S1− trapez ⇔
Suma miar kątów przy ramieniu jest równa 180o.
∡S1+∡s2=180⇔
180−2α+180−2β=180⇔
180=2α+2β
α+β=90o⇔
|∡APB|=90o
II sposób za chwilę.
I sposób
ΔAPS1,ΔBPS2− trójkąty równoramienne
s− wspólna styczna
Czworokąt ABS2S1− trapez ⇔
Suma miar kątów przy ramieniu jest równa 180o.
∡S1+∡s2=180⇔
180−2α+180−2β=180⇔
180=2α+2β
α+β=90o⇔
|∡APB|=90o
II sposób za chwilę.
 II
Kąt między styczną a cięciwą jest równy kątowi wpisanemu opartemu na tej cięciwie,
a odpowiadający kąt środkowy jest dwa razy większy.
2α+2β=180
⇔α+β=90o⇔
|∡APC|=900
II
Kąt między styczną a cięciwą jest równy kątowi wpisanemu opartemu na tej cięciwie,
a odpowiadający kąt środkowy jest dwa razy większy.
2α+2β=180
⇔α+β=90o⇔
|∡APC|=900
 Te okręgi mi nie podeszły.. Ale juz na szczescie koncze planimetrię...
Nie mogę się doczekać aż się zabiorę za arkusze
Te okręgi mi nie podeszły.. Ale juz na szczescie koncze planimetrię...
Nie mogę się doczekać aż się zabiorę za arkusze 

 Wybór Wrocławia
Wybór Wrocławia  był najlepszą decyzją.
Z matematyką jestem na biężąco, pierwsze kolokwium z analizy dopiero po świetach, więc przez
ten okres będę działał
był najlepszą decyzją.
Z matematyką jestem na biężąco, pierwsze kolokwium z analizy dopiero po świetach, więc przez
ten okres będę działał  Algebra to na razie same podstawy − kończymy macierze.
Mam świetnych wykładowców, na razie nie mogę narzekać.
Gorzej z poznawaniem nowych osób − to zdecydowanie na minus.
Pozdrawiam
Algebra to na razie same podstawy − kończymy macierze.
Mam świetnych wykładowców, na razie nie mogę narzekać.
Gorzej z poznawaniem nowych osób − to zdecydowanie na minus.
Pozdrawiam 
 . Tak, została mi końcówka planimetrii,
analityczna, stereo, prawdopodobieństwo i pochodne. Myślę, że od lutego już wezmę arkusze w
dłoń
. Tak, została mi końcówka planimetrii,
analityczna, stereo, prawdopodobieństwo i pochodne. Myślę, że od lutego już wezmę arkusze w
dłoń  . Działam, Ty też będziesz poprawiać?
. Działam, Ty też będziesz poprawiać?
 Jak pewnie wiesz, jestem fanką matematyków wrocławskich.
Jak pewnie wiesz, jestem fanką matematyków wrocławskich.
 Makler Podejdę sobie do matematyki, ale tylko dla własnej satysfakcji(albo i niesaty...
Makler Podejdę sobie do matematyki, ale tylko dla własnej satysfakcji(albo i niesaty... )
)