|x−4|+|2−x|=m
pytanie: |x−4|+|2−x|=m
Kiedy x ma dwa różne dodatnie rozwiązania
16 gru 17:09
===:
to nie x ma rozwiązania tylko równanie.
Nie wypisuj tu własnych bzdetnych interpretacji tylko TREŚĆ ZADANIA ... PRZERYSOWANĄ

16 gru 17:12
Adamm:
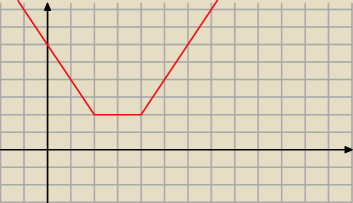
f(x)=|x−4|+|x−2|
równanie teraz ma postać f(x)=m
szukamy kiedy prosta m przecina f(x) w dwóch punktach
f(x)=2x−6 dla x<2
f(x)=2 dla 2≤x<4
f(x)=−2x+6 dla x≥4
widzimy że dla m>2 mamy dwa rozwiązania
16 gru 17:14
pytanie: Wróć, wyznacz wszystkie wartości m , dla których równanie z x ma dokładnie dwa różne
rozwiązania dodatnie
przepraszam

16 gru 17:14
Adamm: nie doczytałem, rozwiązania mają być dodatnie zatem z rysunku mamy
2<m<6
16 gru 17:15
pytanie: Adammie, tam nie powinno być
dla x<2
f(x)=−2x+6
a dla x≥4
f(x)=2x−6?
16 gru 17:18
Adamm: tak
16 gru 17:20
16 gru 17:36

 f(x)=|x−4|+|x−2|
równanie teraz ma postać f(x)=m
szukamy kiedy prosta m przecina f(x) w dwóch punktach
f(x)=2x−6 dla x<2
f(x)=2 dla 2≤x<4
f(x)=−2x+6 dla x≥4
widzimy że dla m>2 mamy dwa rozwiązania
f(x)=|x−4|+|x−2|
równanie teraz ma postać f(x)=m
szukamy kiedy prosta m przecina f(x) w dwóch punktach
f(x)=2x−6 dla x<2
f(x)=2 dla 2≤x<4
f(x)=−2x+6 dla x≥4
widzimy że dla m>2 mamy dwa rozwiązania
