Zadanie optymalizacyjne kuba: Działka ma kształt trójkąta równoramiennego o podstawie długości a i wysokość opuszczoną na tę podstawę długości h. W trójkąt wpisujemy prostokąty tak że jeden z jego boków leży na podstawie trójkąta, a dwa wierzchołki leżą na jego ramionach. Który z tych prostokątów ma największe pole? Ktoś mógłby wytłumaczyć? Kompletna pustka

kuba: pomocy

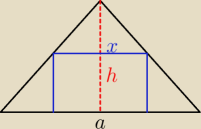
an: wyznacz pole f(x) a następnie max funkcji

===: pół na pół

===:

a		h		a(h−x)
	=		⇒ b=
b		h−x		h

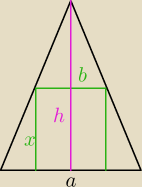
	a(h−x)		a
P=		*x=		(hx−x2)
	h		h

	a		1
P'=		(−2x+h) P'=0 ⇒ x=		h
	h		2

Eta: https://matematykaszkolna.pl/forum/339315.html