algebra_metis
Metis: Algebra
1) Nie wykonując dzielenia, wyznaczyć resztę z dzielenia P(x)= x
4+x
3+x
2+x+1 przez Q(x)=x
2−1
R(x)− szukana reszta z dzielenia
Ponieważ dzielimy przez wielomian stopnia 2 , to R(x) będzie stopnia co najwyżej pierwszego,
mamy zatem:
P(x)= Q(x)*W(x) + R(x), gdzie W(x) jest pewnym wielomianem,
(x−1)(x+1)*W(x)+ax+b= P(x)
Liczę P(1) i P(−1)
P(1)=1+1+1+1+1=5
P(−1)=1−1+1−1+1=1
Stąd:
a+b=5
−a+b=1
2b=6
a=5−a
a=2
b=3
Nasz R(x)=2x+3
Gdzie tutaj element algebry wyższej?

7 gru 19:05
Saizou :
Tutaj chodzi o to aby robić to świadomie, dlaczego możesz zapisać P(x)=Q(x)*W(x)+R(x)
dlaczego można dzielić wielomian przez wielomian itp.
7 gru 20:01
Metis:
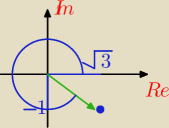
Jak wyznaczamy argument liczby zespolnej z?
Dla przykładu:
(
√3−i)
32.
|z|=
√√32+1=2
| | 11π | |
A w przykładzie podany argument z= |
| |
| | 6 | |
7 gru 20:02
Adamm: ale cosX nie jest różnowartościowy w przedziale <0;2π)
7 gru 20:06
Adamm: | | √3 | |
są 2 takie wartości w przedziale x∊<0;2π) dla których cosx= |
| , dlatego ważne jest w |
| | 2 | |
której
ćwiartce się znajdujemy
7 gru 20:09
Metis: Znajdujemy się w 4

7 gru 20:11
7 gru 20:13
Metis: Zapomniałem o tym, dziękuje

7 gru 20:14
Jack:
(√3−i)32 = ?
(√3−i)3 = ... = − 8i
(√3−i)32 = [(√3−i)3]10 * (√3−i)2 =
= (−8i)10 * (√3−i)2 = 810 * i10 * (3 − 2√3i − 1) =
= 810 * (i2)5 * (2 − 2√3i) = 810 * (−1) * (2 − 2√3i) = 810 * (2√3i − 2) =
= 230 * 2(√3i −1) = 231√3i − 231
7 gru 20:32
Metis:
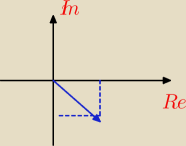
Wyznaczyć i narysować zbiór pierwiastków
3√1−i)6
|z|=
√2
n=3
k=0,1,2
| | δ+2kπ | |
I później zastować wzór na pierwiastki zk=n√|z|(cos |
| + isin... ) |
| | n | |
7 gru 20:34
Metis: Jest

?
7 gru 20:34
Jack: a sinusa nie liczysz

?
7 gru 20:35
7 gru 20:36
Metis: Ktoś potwierdzi?

7 gru 20:44
Metis: Oblicz wyznacznik:
| 1 2 3 4 |
| −1 0 3 4|
|−1 −2 0 4|
|−1 −2 −3 0|
| 1 2 3 4
|0 2 6 8|
|0 0 3 8 |
| 0 0 0 0|
=
1*(−1)
1+1*...
| 2 3 4 |
| 2 6 8 |
|0 3 8|

?

7 gru 20:48
Jack:
wg mnie szybciej :
3√(1−i)6
jednym z rozwiazan rownania na pewno jest (1−i)
2 = 1 − 2i − 1 = −2i
to jest jeden pierwiastek (z 3 jakie istnieja)
zatem
ω
0 = − 2i
pozostale pierwiastki to
| | 2π | | 2π | |
ω1 = ω0 * (cos |
| + i sin |
| ) |
| | n | | n | |
| | 2π | | 2π | |
ω2 = ω1 * (cos |
| + i sin |
| ) |
| | n | | n | |
gdzie n to stopien pierwiastka czyli 3.
7 gru 20:49
Jack:
co do wyznacznika.
druga macierz ( z tych 3 co napisales)
to w ostatniej kolumnie , w ostatnim wierszu ma 4
czyli mamy
|1 2 3 4|
|0 2 6 8|
|0 0 3 8|
|0 0 0 4|
no i wtedy z rozw. Laplace'a
wykreslamy pierwsza kolumne i pierwszy wiersz.
i otrzymujemy 1 * (−1)1+1 *
|2 6 8|
|0 3 8|
|0 0 4|
7 gru 20:53
Jack: jednakze, na glownej przekatnej mamy liczby a pod nia same zera wiec jest to macierz
gornotrojkatna.
wyznacznik takiej macierzyz to iloczyn elementow na przekatnej , czyli wyznacznik to po prostu
1*2*3*4 = 24.
7 gru 20:55
Metis: Racja tam zjadłem 4.
7 gru 20:56
Mila:
z=
3√(1−i)6
z
0=(1−i)
2=−2i
| | 2kπ | | 2kπ | |
zk=(−2i)*(cos |
| +i sin |
| ), k∊{1,2} |
| | 3 | | 3 | |
| | 2π | | 2π | | 1 | | √3 | |
z1=(−2i)*(cos |
| +i sin |
| )=(−2i)*(− |
| +i* |
| ) |
| | 3 | | 3 | | 2 | | 2 | |
z
1=
√3+i
| | 4π | | π | | 1 | | √3 | |
z2=(−2i)*(cos |
| +i sin |
| )=(−2i)*(− |
| −i* |
| ) |
| | 3 | | 3 | | 2 | | 2 | |
z
2=−
√3+i
7 gru 20:57
Metis: Czyli

7 gru 20:57
Metis: Milu a jeśli nie będę mógł odczytać tego pierwszego pierwiastka?
wtedy korzystam z tego wzoru:
http://prntscr.com/dglr7c
7 gru 20:59
Jack: tak, korzystasz z tego, jest uniwersalny.
7 gru 20:59
Metis: Ale czy wtedy zgadza mi się |z| i reszta?
7 gru 21:00
Mila:
Wszystko się zgodzi. Najlepiej będzie, gdy wpiszesz jakiś konkretny przykład.
7 gru 21:06
7 gru 21:08
Mila:
Weźmy ten sam przykład:
z=
3√(1−i)6=
3√(−2i)3=
3√8i
|8i|=8
| | π | |
φ= |
| ( odczytuję z rysunku) |
| | 2 | |
| | | | | |
zk=3√8*(cos |
| +i sin |
| ), k∊{0,1,2} |
| | 3 | | 3 | |
| | π | | π | | √3 | | 1 | |
z0=2*(cos |
| +i sin |
| )=2*( |
| +i |
| )=√3+i |
| | 6 | | 6 | | 2 | | 2 | |
| | 5π | | 5π | | √3 | | 1 | |
z1=2*(cos |
| +i sin |
| )=2*(− |
| +i |
| )=−√3+i |
| | 6 | | 6 | | 2 | | 2 | |
| | 9π | | 9π | | 3π | | 3π | |
z2=2*(cos |
| +i sin |
| )=2*(cos |
| +i sin |
| )=2*(0−i )=−2i |
| | 6 | | 6 | | 2 | | 2 | |
7 gru 21:17
Metis: Pięknie

.
Dziękuje
Milu.
Teraz już rozumiem

7 gru 21:21
Mila:
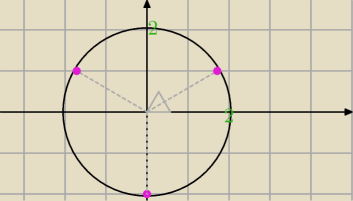
7 gru 21:22
Metis: Milu a jak w tym przypadku policzyć φ bez rysunku?
7 gru 21:28
Jack: jak bez rysunku ?
jak nie ma ani rownania ani rysunku to sie nie da ; D
7 gru 21:31
Mila:
z=3√8i tu chcesz φ obliczyć?
7 gru 21:41
Jack:
chyba, ze masz na mysli jak policzyc kat φ bez rysunku?
No ja np. zawsze licze bez rysunku, bo jest szybciej (wg mnie)
ale jak kto woli, mozna i narysowac.
no to do policzenia bez rysunku potrzebujesz sinus i cosinus oraz modul
jesli mamy np. 8i
no to
|z| =
√02 + 82 = 8
i teraz wg "schemaciku"
1. sprawdzamy znaki przy sin , cos −> widzimy ze oba dodatnie zatem jest to pierwsza cwiartka
| | π | |
2. cosinus przyjmuje 0 dla |
| (wtedy tez sinus przyjmuje jeden) |
| | 2 | |
| | π | | π | |
3. zatem skoro to pierwsza cwiartka to rozwiazanie to |
| czyli φ = |
| |
| | 2 | | 2 | |
7 gru 21:44
Metis: Jaki będzie moduł z=5√(1−i)12 ?
7 gru 22:13
Jack:
w przypadku
(1−i) do potegi dowolnej, rozpisujesz najpierw (1−i)2
a potem uzupelniasz.
w przypadku (√3 ± 1) albo (√3±i) to rozpisujesz do potegi 3.
zatem
(1−i)2 = −2i, czyli
(1−i)12 = ((1−i)2)6 = (−2i)6 = (−2)6 * i6 = 64 * (i2)3 = 64(−1)3 = −64
7 gru 22:15
Metis: |z|=√212=64
7 gru 22:17
jc:
z=(1+i)/√2
(x − z)(x − z3)(x − z5)(x − z7) = ?
7 gru 22:24
Jack: jest

7 gru 22:25
Jack: jc
Mialbym do Ciebie pytanko, a mianowicie : Czy jest jakis wzor na sume kwadratow rozwiazan
rownania zespolonego ?
np. mamy jakis wielomian z4 + ...z3 + ...z2 + ...z + ... = 0
i mamy obliczyc
z12 + z12 + z32 + z44 = ?
7 gru 22:37
jc:
z4+az3+bz2+cz+d=0
z12+z22+z32+z42 = (z1+z2+z3+z4)2−2(z1z2+z1z3+...+z3z4) =
a2−2b
7 gru 22:52
Jack: dzieki

7 gru 22:59
afek: NA akademii sztuk pięknych macie w ogóle matme? i warto tracić na to czas, jak już sesja się
zbliża? no chyba że lajt i w ogóle
8 gru 00:04

 Jak wyznaczamy argument liczby zespolnej z?
Dla przykładu:
(√3−i)32.
|z|=√√32+1=2
Jak wyznaczamy argument liczby zespolnej z?
Dla przykładu:
(√3−i)32.
|z|=√√32+1=2


 Wyznaczyć i narysować zbiór pierwiastków 3√1−i)6
|z|=√2
Wyznaczyć i narysować zbiór pierwiastków 3√1−i)6
|z|=√2
 ?
?
 ?
?

 ?
? 

 .
Dziękuje Milu.
Teraz już rozumiem
.
Dziękuje Milu.
Teraz już rozumiem 


