Nierówność wymierna z parametrem Michał: Dla jakiej wartości parametru k w zbiorze rozwiązań danej nierówności jest zawarty przedział <−1;1>

x2+k2
	≥ 1
2k(6+x)

Jack: https://matematykaszkolna.pl/forum/208437.html

Michał: Podobne, ale jest tam inna nierówność. Bardzo proszę o rozwiązanie dla tej nierówności

Milo: Licznik jest dodatni (k≠0) i wynik ma być dodatni, więc mianownik też musi być dodatni. 2k(6+x) > 0 k>0 i x+6 > 0 lub k<0 i x+6<0 k>0 i x>−6 lub k<0 i x<−6 x² + k² ≥12k + 2kx x² − 2kx +k(k−12) ≥ 0 Δ = 4k² − 4k(k−12) = 4k(k − k + 12) = 48k Oczywiście interesuje nas tylko przypadek, gdy Δ>0 (bo tylko wtedy x>−6 spełniają nierówność). Parabola ma ramiona skierowane ku górze i ma miejsca zerowe, chcemy więc, aby miejsca zerowe były (oba) większe od 1 albo mniejsze od −1 (bo przedział między miejscami zerowymi będzie tym, który nierówności nie spełnia). Jakimś pomysłem jest na pewno wyznaczenie miejsc zerowych z delty i postawienie im tych warunków osobno, ciekaw jestem jednak, czy starczy Viete: x₁ > 1 i x₂ > 1 lub x₁ < −1 i x₂ < −1 x₁ + x₂ > 2 x₁ + x₂ < −2 x₁x₂>1 x₁x₂ > 1 Te warunki na pewno nie są wystarczające, ale gdyby dodać do pierwszego przypadku jeszcze:

1		1
	< 1 i		<1
x1		x2

1		1
	+		< 2
x1		x2

x1 + x2
	< 2
x1x2

To może...? (Do drugiego analogicznie). Wiesz, jaka powinna być odpowiedź? Sam jestem ciekaw, czy mój tok myślenia jest dobry.

Michał: Milo − dziękuję bardzo za odpowiedź, na pewno jest poprawnie do wersu "Jakimś pomysłem", Ogólnie chodzi o to, że to zadanie było na lekcji, na której byłem nieobecny. Jak się pytałem innych to nauczyciel mówił żeby rozpatrzyć położenie wierzchołka. Jutro się dopytam..

Michał: Odp. k∊<7+4√3, +∞)

Kacper:

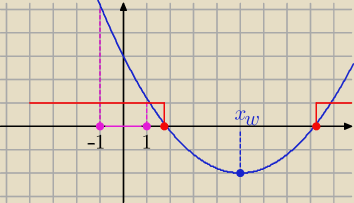
Eta: x∊<−1,1> taka nierówność dla 2k<0 i x+6<0 ⇒ k<0 i x< −6 nie jest spełniona bo x∉<−1,1> dla 2k>0 i x+6>0 ⇒ k>0 i x> −6 dla k>0 x>−6∊<−1,1> zatem możemy mnożyć obustronnie podaną nierówność przez 2k(x+6)>0 otrzymując nierówność: x²−2kx+k²−12k≥0 , Δ= ... =48k >0 −−− są dwa miejsca zerowe

	2k
parabola ramionami do góry , xw=		= k zatem k>1 by x∊<−1,1>
	2

Mamy tylko jedną taką sytuację , którą przedstawiłam na rys. wyżej zatem parametr "k" musi spełniać układ warunków: Δ>0 −−− spełniony bo Δ= 48k i k>1 x_w>1 ⇒ k>1 f(1)≥0 ⇒ ....... k²−14k+1≥0 ⇒ ....... k∊<7+4√3,∞) bo k>1 f(−1) ≥0 ⇒ ..... k²−10k+1≥0 ⇒ ...... k∊<5+2√6, ∞) bo k>1 wybierając część wspólną otrzymujemy Odp: k∊< 7+4√3, ∞)

Eta: Hej Kacper Czy to może Twój uczeń ?

Michał : Dziękuję Eta

Kacper: Nie Gdyby był mój to by miał 1