aa
PrzyszlyMakler: Witam, mam dwa pytania, pierwsze takie ogólniejsze.
1. Jak to jest z mnożeniem nierówności na krzyż? Co musze wiedzieć itd. Co po której stronie
itp.
2. Taka nierówność
| 1−√3 + 3tgx + √3tgx | |
| ≤0 |
| 2(1−tgx) | |
I przyznam szczerze, że nie wiem jak to zrobić.Zrobiłem w ten sposób:
1−
√3 + 3tgx +
√3tgx=0
| | √3 | |
Po rozwiązaniu tgx = |
| , ale jak to teraz zapisać i rozwiążać? Bo skoro to nierownosc, |
| | 3 | |
a w mianowiku jest −tgx, czyli x przy najwyższej potędze jest ujemne to będę zaczynał rysować
graf nierówności od dołu, pomoże ktoś>?
27 lis 16:21
Omikron: 1. Musisz po prostu sprawdzić czy wyrażenia przez które mnożysz są dodatnie czy ujemne i w
razie czego zmienić kierunek nierówności.
2. Wymnóż przez kwadrat mianownika. Za tgx podstaw t i doprowadź do postaci iloczynowej, potem
wróć do tgx
27 lis 17:01
Mila:
tgx≠1 i cosx≠0
[1−
√3+tgx*(3+
√3)]*(1−tgx)≤0⇔
[1−
√3+tgx*(3+
√3)]≥0 i (1−tgx)<0 lub [1−
√3+tgx*(3+
√3)]≤0 i (1−tgx)>0⇔
(3+
√3)*tgx≥
√3−1 i 1<tgx lub (3+
√3)*tgx≤
√3−1 i 1>tgx
Licz dalej sam
27 lis 17:23
PrzyszlyMakler: Tamten przykład już rozumiem. Potrzebuję pomocy z takim czymś:
Rozwiąż nierówność 1 + log
2(sin2x) + log
2(sin2x)
2 + .... < 0,(6) w zbiorze <0;2π> gdzie lewa
strona jest zbieżnym szeregiem geometrycznym.
q = log
2sin2x należy (−1;1)
| | π | | 5 | | 13 | | 17 | |
D: x ∊( |
| ; |
| π)u( |
| π ; |
| π) |
| | 12 | | 12 | | 12 | | 12 | |
| | 1 | |
Suma lewej strony mi wyszła: |
| |
| | | |
po wielu operacjach wyszło mi:
2(1−
√2sin2x)sin2x > 0
No i teraz najfajniejsza zabawa:
√2sin2x = 1
| | π | | 3 | |
x = |
| + kπ lub x = |
| π + kπ |
| | 8 | | 8 | |
sin2x = 0
x = {π}{2}k
Czyli WSZYSTKIE miejsca zerowe na przedziale 0;2pi to:
| | π | | 3 | | 1 | | 9 | | 11 | | 3 | |
x0 = { |
| , |
| π, |
| π ,π , |
| π , |
| π , |
| π , 2π} |
| | 8 | | 8 | | 2 | | 8 | | 8 | | 2 | |
| | π | | 5 | | 13 | | 17 | |
D: x ∊( |
| ; |
| π)u( |
| π ; |
| π) |
| | 12 | | 12 | | 12 | | 12 | |
Nierówność jest postaci:
2(1−
√2sin2x)sin2x > 0 Więc WYDAJE MI SIĘ, że powinienem zacząć szkicować wykres OD DOŁU,
ale po narysowaniu wszystkich miejsc zerowych i zaczęciu od DOŁU juz widzę, że wychodzi źle
[nie pokrywa się z odpowiedzią],
a jakbym zaczął rysować od góry to mam dokładnie tak jak w odpowiedzi. Ale dlaczego od góry a
nie od dołu

Trzeba rozwiązać na przedziale <0;2π>
27 lis 18:04
PrzyszlyMakler: Pomoccyyyyyy

27 lis 18:51
PrzyszlyMakler: Bardzo ładnie proszę o pomoc. Tylko tę końcówkę rozjasnić.. wydaje mi się, że wszystko dobrze
policzone.
27 lis 19:06
PrzyszlyMakler: Sorki za spam, ale to "blokuje" mój rozwój matematyczny..

27 lis 19:15
27 lis 19:15
Mila:
Za godzinę będę wolna. Teraz mam gości.
27 lis 19:18
PrzyszlyMakler: Oki, grunt abyś znalazła chwilkę żeby mi pomóc, Wspaniała Milu

. Z góry dziękuję, bo
normalnie liczę to zadanie, wychodzi źle, patrzę na internet i nigdzie go nie ma, to liczę
jeszcze raz i doszedłem do tego 'błedu' i masa frustracji.

27 lis 19:23
PrzyszlyMakler: Przezywam załamanie! Rysuje sobie wykres mojej funkcji tj. 2(1−sqrt(2)sin(2x))*sin(2x) jakimś
programem i wychodzi dobrze, czyli zacyznają od góry, ale jakim prawem, skoro powinno się od
dołu?
27 lis 20:22
Mila:
Czy chodzi o rozwiązanie nierówności w przedziale <0,2π> ?
2(1−√2*sin2x)*sin2x > 0
27 lis 21:16
PrzyszlyMakler: tak, a dokładnie jak wiedzieć skąd zaczynać rysowanie wykresu bo wszystkie miejsca zerowe mam.
27 lis 21:40
Omikron: Niech t=sin2x i t∊<−1,1>
(1−
√2t)t>0
Odczytujesz z wykresu rozwiązanie.
Dalej prosto.
27 lis 21:56
Mila:
Liczę wszystko od początku:
Czekaj. Możesz napisać tymczasem odpowiedź, jeśli masz.
27 lis 22:15
PrzyszlyMakler: | | π | | π | | 3 | | 5 | | 13 | | 9 | | 11 | | 17 | |
x ∊ ( |
| ; |
| )u( |
| π; |
| π)u( |
| π; |
| π)u( |
| π; |
| π) |
| | 12 | | 8 | | 8 | | 12 | | 12 | | 8 | | 8 | | 12 | |
27 lis 22:26
Mila:
Zgadza się zaraz napiszę.
27 lis 22:29
PrzyszlyMakler: Milu, ale ja to zadanie zrobiłem dobrze, nawet jak rysuję programem funkcję to jest dobrze.
Tylko ja nie wiem skąd mam wiedzieć czy z góry czy z dołu rysować wykres tej nierówności.

27 lis 22:30
Mila:
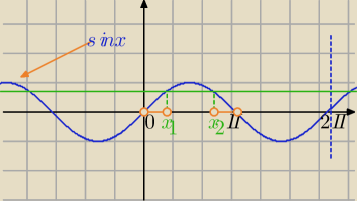
szereg geometryczny z logarytmem
| | π | | 5π | | 13π | | 17π | |
1) Dziedzina dobrze ustalona: x∊( |
| , |
| )∪( |
| , |
| ) |
| | 12 | | 12 | | 12 | | 12 | |
2)Nierówność :
(1−
√2*sin(2x))*sin(2x)>0
Ponieważ sin(2x)>0 z założenia, to
(1−
√2*sin(2x))>0 i x∊D⇔
| | π | | 3π | |
0+2kπ<2x< |
| +2kπ lub |
| +2kπ<2x<π+2kπ /:2 |
| | 4 | | 4 | |
| | π | | 3π | | π | |
kπ<x< |
| +kπ lub |
| +kπ<x< |
| +kπ i x∊D |
| | 8 | | 8 | | 2 | |
k=0
k=1
| | 9π | | 11π | | 3π | |
x∊(π, |
| )∪( |
| , |
| ) |
| | 8 | | 8 | | 2 | |
teraz część wspólna z D
Narysować oś w drugim wątku?
27 lis 22:30
PrzyszlyMakler: Analizuję. A co oznacz to: "Ponieważ sin(2x)>0 z założenia"
27 lis 22:39
Mila:
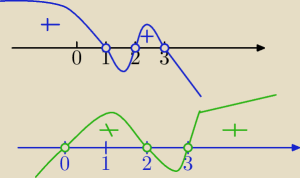
Przykład
1) (x−1)*(x−2)*(3−x)>0
po wymnożeniu ( w pamięci) patrzysz znak przy x
3 :
Mamy (−x
3)
x∊(−
∞,1)∪(2,3)
2)
x*(x−2)*(x−3)>0
27 lis 22:40
Mila:
Wcześnie ustaliłeś, że sin(2x)>0 i podałeś dziedzinę w której zachodzi ten warunek:
Aby iloczyn
(1−√2*sin(2x))*sin(2x)>0 to drugi czynnik tez musi być większy od zera.
27 lis 22:43
PrzyszlyMakler:
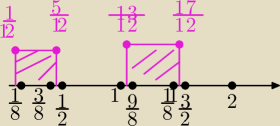
Wszystkie punkty na grafie mają przy sobie π. Na fioletowo dziedzina.
Rozwiązanie nieroówności (1−
√2sin2x)sin2x>0 zrobiłem w ten sposób, że zaznaczyłem wszystkie
punkty na osi wraz z dziedziną. I moim jedynym problemem przy rozwiązaniu tego zadania było,
że nie wiem czy od dołu czy od góry zacząć rysować graf. Współczynnik przy najwyższej potędze
jest ujemny czyli z prawej strony od dołu ale gdy tak zrobiłem to było źle. Muszę od góry i
wtedy wychodzi wynik jak w odpowiedziach, ale nie wiem dlaczego od góry, Milu.

27 lis 22:51
Mila:
Tu masz nierówność trygonometryczną i postępujesz inaczej.
Jeżeli nie chcesz skorzystać z mojej wskazówki, to trzeba rozwiązać tak:
(1−√2sin(x)) >0 i sin(2x)>0 lub (1−√2sin(x)) <0 i sin(2x)<0 ( to sprzeczne z założeniem)
27 lis 22:55
PrzyszlyMakler: właśnie Cię chciałem zapytać dlaczego nie rozpatrujemy przypadku gdy oba są ujemne?
27 lis 23:02
Mila:
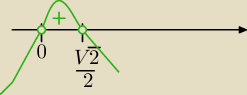
Możesz zastosować podstawienie:
(1−
√2t)*t>0
| | √2 | |
sin(2x)>0 i sin(2x)< |
| i wychodzi na to co podałam 22:30. |
| | 2 | |
27 lis 23:04
Mila:
Możesz rozważyć , że obydwa czynniki są ujemne, zobaczysz co dostaniesz.
27 lis 23:08
PrzyszlyMakler: Nie wiem Milu, dziś siedzę bardzo długo już i nie myślę i rozumiem, że jeżeli a*b>0 to a i b >
0 lub a i b < 0 ale nie wiem dlaczego Ty drugi przypadek nie rozważasz i nie wiem skąd
założyłaś, że sin2x >0 Musze jutro przeanalizować to wszystko bo teraz tylko się denerwuję,
dziękuję Ci za wszystko za wszystkie chęci, jutro to jeszcze wszystko przeczytam i dam 100% ze
swojego mózgu, aby Twoja pomoc nie była daremna. Dziękuję raz jeszcze, jeżeli możesz to możesz
odpowiedzieć jeszcze raz jakoś bardzo nieziemsko prosto na te pytania, a jak nie to mam
nadzieje, ze jutro sam do tego dojdę.
27 lis 23:17
Mila:
Masz wyrażenie:
log2(sin(2x)) i wiadomo, że liczba logarytmowana musi być większa od zera
i to na samym początku trzeba założyć , wyznaczyć dziedzinę tego wyrażenia.
Jeżeli rozważysz drugi przypadek : obydwa czynniki ujemne to dostaniesz sprzeczność,
ja to widzę "do przodu" i dlatego nie rozwiązuję.
Jeżeli Ty nie widzisz, to rozwiąż.
Spokojnie. Wyjdzie wszystko dobrze.
Możesz zostawić to zadanie na jakiś czas, daj czerwoną gwiazdkę,
wróć do niego po pewnym czasie.
27 lis 23:35
PrzyszlyMakler: już rozumiem, no tak liczba logarytmowana musi być większa od 0, więc wystarczy rozwiązać to z
pierwiastkiem, Dziękuję

Naprawdę wczoraj nic nie mogłem dostrzec

. Dziękuję Milu, jesteś
najlepsza

28 lis 12:11
5-latek: A
Eta ?

Do ktorej Pani powiesz ze jest najlepsza ?
28 lis 12:17
 Trzeba rozwiązać na przedziale <0;2π>
Trzeba rozwiązać na przedziale <0;2π>


 . Z góry dziękuję, bo
normalnie liczę to zadanie, wychodzi źle, patrzę na internet i nigdzie go nie ma, to liczę
jeszcze raz i doszedłem do tego 'błedu' i masa frustracji.
. Z góry dziękuję, bo
normalnie liczę to zadanie, wychodzi źle, patrzę na internet i nigdzie go nie ma, to liczę
jeszcze raz i doszedłem do tego 'błedu' i masa frustracji. 

 szereg geometryczny z logarytmem
szereg geometryczny z logarytmem
 Przykład
1) (x−1)*(x−2)*(3−x)>0
po wymnożeniu ( w pamięci) patrzysz znak przy x3 :
Mamy (−x3)
x∊(−∞,1)∪(2,3)
2)
x*(x−2)*(x−3)>0
Przykład
1) (x−1)*(x−2)*(3−x)>0
po wymnożeniu ( w pamięci) patrzysz znak przy x3 :
Mamy (−x3)
x∊(−∞,1)∪(2,3)
2)
x*(x−2)*(x−3)>0
 Wszystkie punkty na grafie mają przy sobie π. Na fioletowo dziedzina.
Rozwiązanie nieroówności (1−√2sin2x)sin2x>0 zrobiłem w ten sposób, że zaznaczyłem wszystkie
punkty na osi wraz z dziedziną. I moim jedynym problemem przy rozwiązaniu tego zadania było,
że nie wiem czy od dołu czy od góry zacząć rysować graf. Współczynnik przy najwyższej potędze
jest ujemny czyli z prawej strony od dołu ale gdy tak zrobiłem to było źle. Muszę od góry i
wtedy wychodzi wynik jak w odpowiedziach, ale nie wiem dlaczego od góry, Milu.
Wszystkie punkty na grafie mają przy sobie π. Na fioletowo dziedzina.
Rozwiązanie nieroówności (1−√2sin2x)sin2x>0 zrobiłem w ten sposób, że zaznaczyłem wszystkie
punkty na osi wraz z dziedziną. I moim jedynym problemem przy rozwiązaniu tego zadania było,
że nie wiem czy od dołu czy od góry zacząć rysować graf. Współczynnik przy najwyższej potędze
jest ujemny czyli z prawej strony od dołu ale gdy tak zrobiłem to było źle. Muszę od góry i
wtedy wychodzi wynik jak w odpowiedziach, ale nie wiem dlaczego od góry, Milu.
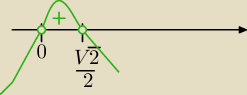 Możesz zastosować podstawienie:
(1−√2t)*t>0
Możesz zastosować podstawienie:
(1−√2t)*t>0
 Naprawdę wczoraj nic nie mogłem dostrzec
Naprawdę wczoraj nic nie mogłem dostrzec  . Dziękuję Milu, jesteś
najlepsza
. Dziękuję Milu, jesteś
najlepsza 
 Do ktorej Pani powiesz ze jest najlepsza ?
Do ktorej Pani powiesz ze jest najlepsza ?