trójmian kwadratowy, parametr m
neiii: Dany jest trójmian kwadratowy w określony dla x∊R wzorem
w(x) = (m − 4)x2 + (m + 2)x + m + 2.
Funkcja f przyporządkowuje każdej wartości rzeczywistej m iloczyn pierwiastków
rzeczywistych równania kwadratowego w(x) = 0. Narysuj wykres funkcji f.
24 lis 21:00
Kacper:
Jak dla mnie równanie ma rozwiązania nie pierwiastki.
Δ>0 ⇒ równanie ma dwa rozwiązania o iloczynie...
Δ=0 ⇒ równanie ma jedno rozwiązanie
Zapewne moje rozwiązanie nie zgodzi się w tym w odpowiedziach

Chętnie posłucham wypowiedzi
PW, bo mamy podobne poglądy w tej kwestii

24 lis 21:09
===:
licz deltę ...ustalaj przedział Δ>0 ⋀ m−4≠0 ... i to będzie jednocześnie dziedzina dla f(m)
masz f.homograficzną... przekształć do postaci kanonicznej i rysuj (nie zapomnij o wyżej
wyznaczonej dziedzinie
24 lis 21:14
neiii: ok, dziękuję

24 lis 21:15
===:
Bardzo zdziwiłbym się Kacper gdyby PW podzielił Twój pogląd.
1. Rozwiązanie równania to inaczej pierwiastki.
2. Δ=0 to jeden pierwiastek (podwójny)
24 lis 21:26
===:
ale w sprawie 2. trwa dyskusja stara jak świat

Skoro nie ma w treści dwa różne pierwiastki ... to można dyskutować

24 lis 21:29
PW: Czy ktoś wpadłby na pomysł, żeby powiedzieć:
− Równanie
sin2x + 2sinx + 1 = 0
ma w przedziale (0, π) pierwiastek podwójny?
24 lis 21:41
===:
Ten przykład chyba nie bardzo tu pasi. Jeśli rozpatrujesz równanie względem sinx
to ma pierwiastek podwójny sinx=−1 W podanym przedziale sinx takiej wartości nie przyjmuje.
Jeśli względem x ... to zupełnie inna bajka
24 lis 22:09
PW: Tak, miało być − 2sinx. Ale powiedziałbyś, że jest to pierwiastek podwójny?
24 lis 22:20
Kacper:
Ja będę się spierał i mówił, że równanie ma rozwiązania, a wielomiany mają pierwiastki

Kwestia gustu

Pytanie jak mam liczyć sumę jednego pierwiastka (podwójnego)? Nie uczyli mnie obliczać sumy
jednej liczby

24 lis 22:25
===:
t
2+2t+1=0 jest równaniem kwadratowym i ma ono pierwiastek podwójny
sin
2x+2sinx+1=0 jako równanie względem x równaniem kwadratowym nie jest

24 lis 22:26
===:
o jakiej Ty sumie
Kacper mówisz

Zresztą zaprzeczasz sam sobie
24 lis 22:28
piotr: rozwiązanie równania zawsze jest jedno, a może ono się składać z wielu pierwiastków (mówi się
również o zerach wielomianów)
24 lis 22:43
PW: Tylko wielomiany miewają pierwiastki wielokrotne.
Równania miewają rozwiązania. Użycie liczby mnogiej − "rozwiązania" − oznacza, że jest ich
więcej niż jedno.
Przy takim rozumieniu nie ma głupich dyskusji.
Dlaczego mówimy "zbiór rozwiązań nierówności" (tak jest w materiałach CKE), a gdy pojawia się
równanie − zwłaszcza z wielomianem − to zaczynamy mówić o pierwiastkach, w dodatku
"podwójnych"? To relikt lat minionych bardzo − pamiętam takie "podchwytliwe" zadania, kiedy
łapało się ucznia na tych niuansach niesłusznie.
Korzystamy ze starych zbiorów zadań bez przeredagowania treści. Jestem przekonany, że sprawa
została już dawno uregulowana. Jeśli mam błędne przekonanie, to na pewno eksperci minister
Zalewskiej to wyprostują.
24 lis 22:59
piotr: | | m+2 | | 6 | |
f(m) = |
| = 1 + |
| |
| | m−4 | | m−4 | |
24 lis 23:00
piotr:
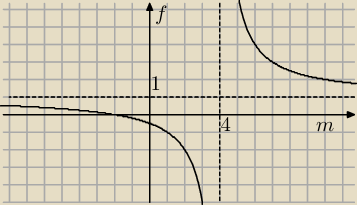
24 lis 23:02
PW: https://matematykaszkolna.pl/strona/4427.html
W materiałach CKE używa się określeń "rozwiązanie równania" i "pierwiastki trójmianu".
Natomiast Operon (i dziwię się temu) nawet w tegorocznej maturze pisze o pierwiastkach
równania.
24 lis 23:21
===:
To co teraz wypisujesz Szanowny PW to już po trosze herezje.
Nikt w tym wątku przed Tobą nie użył określenia głupia dyskusja ... ale teraz rzeczywiście
robi się ona głupia. Matematyka jest nauką ścisłą ... pewne określenia (język) ustalono już
dawno ... ale to właśnie teraz "każdy wszystko może" ... i tak powstaje chaos.
Broniąc tego co wypisujesz "chytasz" się przepraszam za określenie ale bredni.
"Dlaczego mówimy "zbiór rozwiązań nierówności" ... bo przecież najczęściej rozwiązaniem bywa
zbiór ... zbiór argumentów dla których nierówność jest spełniona. Bywa, że zbiór ten
jest jednoelementowy bądź pusty.
Argumenty dla których funkcja przyjmuje wartość 0 ... to miejsca zerowe
W odniesieniu do równań ich rozwiązania to pierwiastki
Sięgnij do opracowań naukowych i tam znajdziesz określenie "pierwiastek dwukrotny" przez
innych określany jako podwójny. Oczywiście krytykować można wszystko ... klasyków też
i "każdy wszystko dziś może"
24 lis 23:24
PW: ===, ja nie dyskutuję z Tobą, bo się nie da. Już zaczynasz obrażać, nie pierwszy raz. Ja nie
"chytam się bredni", ale mam poglądy i wiedzę, nawet o tym, że matematyka jest nauką ścisłą.
Pozostańmy przy swoich poglądach, bo pobić się nie możemy.
Zostań już sam na tym forum, ja kończę, bo mam poczucie, że marnuję życie.
24 lis 23:33
===:
To już jest chamstwo z Twojej strony. Ty obrażasz a potem zarzucasz to innym
i udajesz cnotę uciśnioną.
24 lis 23:38
Ajtek:
PW i chamstwo? To jest zbiór pusty!
25 lis 00:23
fbfbf:
99% osob ( w tym ja ) nie zalezy na tym jakiego slowa sie uzyje : pierwiastek, rozwiazanie czy
jeszcze co innego. Chodzi o to by wiedziec jak 'rozwiazac' 'obliczyc' dane zadanie.
25 lis 00:53
25 lis 01:16
 Chętnie posłucham wypowiedzi PW, bo mamy podobne poglądy w tej kwestii
Chętnie posłucham wypowiedzi PW, bo mamy podobne poglądy w tej kwestii 

 Skoro nie ma w treści dwa różne pierwiastki ... to można dyskutować
Skoro nie ma w treści dwa różne pierwiastki ... to można dyskutować 
 Kwestia gustu
Kwestia gustu  Pytanie jak mam liczyć sumę jednego pierwiastka (podwójnego)? Nie uczyli mnie obliczać sumy
jednej liczby
Pytanie jak mam liczyć sumę jednego pierwiastka (podwójnego)? Nie uczyli mnie obliczać sumy
jednej liczby 

 Zresztą zaprzeczasz sam sobie
Zresztą zaprzeczasz sam sobie
