oblicz
katix: Trójkąt równoramienny ABC( AC = BC )o obwodzie 64 cm wpisano okrąg . wiedząc że podstawa AB
jest o 4 cm dłuższa od ramienia trójkąta Oblicz pole trójkąta ABC pole koła wpisanego w
trójkąt ABC długość odcinka EF gdzie E i F są punktami styczności ramion trójkąta z okregiem
17 lis 21:47
katix: Tak dokładniej to chodzi mi tylko jak wyliczyć promień

17 lis 22:03
===:
znasz zatem wszystkie boki tego trójkąta ...znasz pole ...znasz promień
17 lis 22:05
Eta:
P=rp p −−− połowa obwodu , P −−pole trojkąta
h= 16 , a= 24 P=192 p=32
17 lis 22:07
katix: Eta dlaczego pole pole podzielić na pół obwodu to jest promień

17 lis 22:15
17 lis 22:21
katix: już dziękuję udało mi się zrobić


17 lis 22:24
Eta:

17 lis 22:26
Mila:
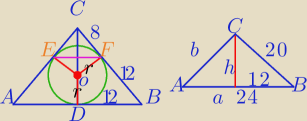
1)
a=b+4
b+4+2b=64
3b=60
b=20
a=24
h
2+12
2=20
2
h
2=400−144=256
h=16
2)
P
Δ=p*r, gdzie p− połowa obwodu Δ
192=32r
r=6
3)ΔCEF∼ΔABC⇔
dokończ
17 lis 22:26
Eta:
I już
Mila ............Cię wyręczyła ( czyli ... "podała na tacy"

17 lis 22:27
katix: dziękuję bardzo

17 lis 22:29
===:
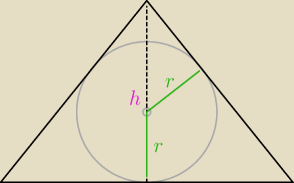
nie chcesz tak ... to licz z podobieństwa trójkątów
h=
√256=16
17 lis 22:29





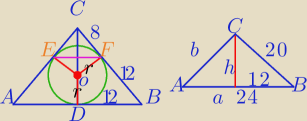 1)
a=b+4
b+4+2b=64
3b=60
b=20
a=24
h2+122=202
h2=400−144=256
h=16
1)
a=b+4
b+4+2b=64
3b=60
b=20
a=24
h2+122=202
h2=400−144=256
h=16


 nie chcesz tak ... to licz z podobieństwa trójkątów
h=√256=16
nie chcesz tak ... to licz z podobieństwa trójkątów
h=√256=16