równanie z parametrem
Gosia: Bardzo proszę o pomoc...
Zbadaj liczbę rozwiązań równania: | | x − 2 | + 3 | = 2m + 4 w zależności od parametru m.
10 sty 22:23
paziówna: ja zrobię
10 sty 22:26
Gosia: będę bardzo wdzięczna
10 sty 22:29
paziówna:
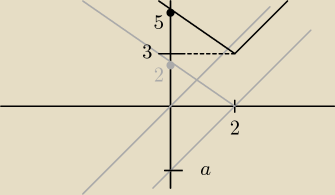
a = −2
y = x → y = x − 2 → y = |x − 2| → y = |x − 2| + 3 → f(x) = ||x − 2| + 3|
0 rozwiązań:
2m + 4 < 3
1 rozwiązanie
2m + 4 = 3
2 rozwiązania
2m + 4 > 3
10 sty 22:35
paziówna: jeśli chcesz, mogę Ci jeszcze opisać przekształcenia, które wykonałam na funkcji y = x
10 sty 22:35
Gosia: nie do końca wiem co i jak z tym wykresem.. ?
10 sty 22:41
paziówna: no więc właśnie. tam porobiłam przekształcenia izometryczne.
najpierw zrobiłam translację o wektor [0, −2](może też być [2, 0] tutaj nie ma to znaczenia),
stąd y = x −2. następnie symetrię częściową względem OX dla y>0(stąd moduł). później znów
translacja o wektor [ 0, 3] i na koniec znów częściowa symetria względem OX dla y>0.
10 sty 22:45
Gosia: ałłaa.. to wyższa matematyka jak dla mnie. Spróbuje gdzieś o tych przekształceniach poczytać i
moze mi sie rozjaśni, bo jakby tak zechcieli sprawdzić samodzielność rozwiązania... ale dzięki
wielkie
10 sty 22:49
paziówna: a tak z ciekawości − poziom podstawowy czy poziom rozszerzony?
10 sty 23:02
Gosia: ja podstawowy, a zadanie pewnie z rozszerzenia bo nie słyszałam nawet o takich
przekształceniach?
10 sty 23:04
paziówna: no właśnie... więc skąd Ty wzięłaś to zadanie?
10 sty 23:09
Gosia: ano, jest do zrobienia i już. Ciiicho bo nie powinnam tu wchodzić w ogóle z nim
10 sty 23:10
paziówna: oj tam, każdy tu wrzuca swoją pracę domową^^
10 sty 23:12
Gosia: to nie jest bynajmniej praca domowa
ale, że mam jakiś tam przerost ambicji, ja sie dowiem o
co chodzi z tymi przekształceniami i oddam to zadanie, haha
10 sty 23:14
paziówna: żaden przerost ambicji, chcesz wiedzieć, co z czego wynika. pochwalam!
10 sty 23:22
10 sty 23:26
Gosia: Hmm to jakby coś mi świeci już, jakieś było tylko nie nazwane przekształceniem izometrycznym
no i nie z wartością bezwzględną. A ja jak widzę wartość bezwzględną to odpuszczam zazwyczaj
10 sty 23:47
paziówna: no coś Ty, dlaczego? ale wiesz, na przyszłość, moduły są wszędzie, gdzie tylko się da, więc
lepiej się z nimi oswoić
10 sty 23:50
Gosia: bo zazwyczaj każde rozwiązanie z modułem w moim wykonaniu jest źle, ale może kiedyś się
nauczę
11 sty 21:53