bryły Slawa: W ostrosłupie prawidłowym trójkątnym kąt płaski przy wierzchołku ma miarę α. Oblicz cosinus kąta zawartego między dwoma sąsiednimi ścianami bocznymi tego ostrosłupa jeśli

	7
cosα = −
	25

	7
Gdy cosα=		to umiem rozwiązać ale gdy kąt płaski jest rozwarty mam problem
	25

	7
Odp ma być −
	18

Eta:

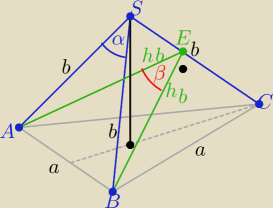
	7		24
cosα= −		to sinα=		i b>0
	25		25

P(ABS) =P(BCS)=P(ACS)

	b2*sinα		1
P(ABS)=		i P(BCS)=		b*hb
	2		2

	24
to porównując pola : hb=		b
	25

	7
Z twierdzenia kosinusów w ΔABS : a2= 2b2+2b2*		⇒ a2=.....
	25

i z twierdzenia cosinusów w ΔABE :

	2hb2−a2		7
cosβ=		=.................... = −
	2hb2		18

Slawa: Właśnie nie rozumiem bo ΔBCS jest rozwarty więc wysokość h_b nie leży w płaszczyźnie trójkąta BCS. Wg mnie rysunek nie jest adekwatny do warunków zadania.

Eta: https://matematykaszkolna.pl/forum/266564.html Tu masz ładne wyprowadzenie przez Bogdanawzoru na:

	cosα
cosβ=
	1+cosα

	7
podstawiając za cosα= −
	25

	7   −   25		7
cosβ=		= .... = −
	7   1−   25		18

Slawa: Tzn że gdy trójkąty ścian bocznych są rozwartokątne to kąt między nimi liczymy tak, że ze środków podstawy wyprowadzamy prostopadłe do krawędzi bocznych i mamy kąt. Nie wiedziałam tego