ostrosłup Blue: W ostrosłupie prawidłowym trójkątnym kąt płaski przy wierzchołku ma miarę α. Oblicz cosinus kąta zawartego między dwoma sąsiednimi ścianami bocznymi tego ostrosłupa, jeśli:

	7
a) cosα=
	25

Blue:

Blue: Eta, Mila?

Tadeusz:

	1
sin(β/2)=
	2cos(α/2)

dalej sobie przekształć −

Eta:

	7
Z moich obliczeń cosγ=
	32

Raf131:

	7
Potwierdzam też mam wynik
	32

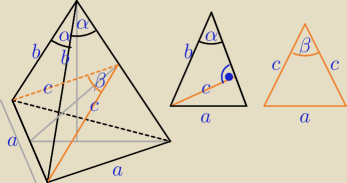
Bogdan: Warto pokazać obliczenia do tego zadania. c = bsinα ⇒ c² = b²sin²α = b²(1 − cos²α) = b²(1 − cosα)(1 + cosα) Z twierdzenia cosinusów: a² = 2b² − 2b²cosα i a² = 2c² − 2c²cosβ 2b²(1 − cosα) = b²(1 − cosα)(1 + cosα)(1 − cosβ) Po uproszczeniu przez 2b²(1 − cosα): 1 = (1 + cosα)(1 − cosβ)

	1		1		cosα
1 − cosβ =		⇒ cosβ = 1 −		=
	1 + cosα		1 + cosα		1 + cosα

	7		7     25		25		7
dla cosα =		mamy cosβ =		*		=
	25		7   1 +   25		25		32

Blue: Bogdan − wielkie dzięki

Eta:

Blue:

	7
mam tutaj jeszcze podpunkt b) cosα= −		, to teraz nie mogę tego tak liczyć Bo jest kąt
	25

rozwarty...Tylko że jak podstawiłam do tego ostatniego wzoru, który Ci wyszedł, to wyszedł dobry wynik... Wiec nie wiem, czy tak można?

Blue: Co Eta

Blue: Może ktoś wyjaśnić ten podpunkt z kątem rozwartym

Bogdan: Wzór jest ogólny i dla dowolnych wartości cosα.

	cosα		7   −   25		25		7
cosβ =		=		*		= −
	1 + cosα		7   1 −   25		25		18

Bogdan: oczywiście α∊(0^o, 180^o)

Blue: Hmmm... a więc to tak, ale jednak czy wtedy ta własność z sinusem jest poprawna: c = bsinα

Blue: Bogdan, a jakbyś nie miał tego wzoru wyliczonego i musiał dojść do wszystkiego od początku w tym drugim podpunkcie, to liczyłbyś wszystko tak samo?

Blue:

Blue: Eh... dziwne mi się to wydaje, ale nich będzie..

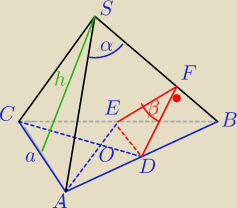
Mila: Liczysz cos ∡EFD.

Mila: Ozn. |AB|=a DB=a ED||AC, |ED|=a WΔSAB:

	α
∡ABS=900−
	2

WΔDFB:

	α		DF
sin(B)=sin(900−		)=		⇔
	2		DB

	α		DF
cos		=
	2		a

	α
|DF|=a*cos
	2

==========

	7		α
cosα=−		=2cos2		−1⇔
	25		2

	α		18
2cos2		=
	2		25

Z tw. cosinusów , w ΔEDF:

	α		α		α
a2=a2*cos2		+a2*cos2		−2a2*cos2		*cosβ /:a2⇔
	2		2		2

	α		α
1=2*cos2		−2*cos2		*cosβ
	2		2

	18		18
1=		−		cosβ
	25		25

7		18
	=−		cosβ
25		25

	−7
cosβ=
	18

Mila: ?

Blue: Nie ogarniam tego twierdzenia cosinusów..

Blue: To zadanie jest strasznie zagmatwane

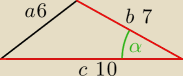
Mila: Nie żartuj. Napisz kilka przykladów i opanujesz. Obejmujesz kąt raminami i: a²=c²+b²−2*b*c*cosα

Kacper:

Blue: Zaraz będę to jeszcze raz ogarniać, ale chcę najpierw skończyć tą trygonometrię

Blue: Mila źle mnie zrozumiałaś − ogarniam tw.cosinusów ogólnie, ale mi chodzi o to tutaj konkretne, które zapisałaś

Mila: Czytaj kilka razy, przepisz na kartkę, na pewno zrozumiesz, musisz umieć liczyc na wzorkach.

Blue: Mila może zacznijmy od tego, że napisałaś : "Ozn. |AB|=a DB=a" , a to przecież samo sobie zaprzecza

Blue: Dobra, przeanalizowałam to jeszcze raz i nie rozumiem tego : |ED|=|BD| − dlaczego tak

Mila: Poprawiam 23:09 No oczywiście Ozn. |AB|=2a , |AC|=2a |BC|=2a

Mila: ΔEBD− Δrównoboczny.

Mila: Albo

	1
ED odcinek łączący środki boków Δ⇔ED||CA i |ED|=		|AC| ( Pan Tales Cię pozdrawia)
	2

Blue: No tak teraz wszystko jasne i oczywiste Dziękuję

Roler: Z twierdzenia cosinusów: a2 = 2b2 − 2b2cosα i a2 = 2c2 − 2c2cosβ 2b2(1 − cosα) = b2(1 − cosα)(1 + cosα)(1 − cosβ) Może ktoś to rozpisać dlaczego tak jest?

Aniax2: Tam powinna być dwójka przy b² po prawej stronie równania już przy wyznaczaniu cosα i cosβ w jednej linii. To może wprowadzać w błąd i niektórzy nie wiedzą skąd to się bierze. Wykorzystujemy 2 równania z 'a' i 1 z 'c'

Kacper: Ładny dinozaur, odkopany po 5 latach

Kamil: Super!