tryg zef:

	√2
sin3x=−
	2

	5π		5π
3x=		+2kπ lub 3x=π−		+2kπ
	4		4

	5π		2		π		2
x=		+		kπ lub x=−		+		kπ
	12		3		12		3

Może ktoś sprawdzić czy się wszystko tutaj zgadza ?

PW: W zakresie od 0 do 2π:

	π		5
3x = π +		=		π − dobrze
	4		4

lub

	π		7
3x = 2π −		=		π − tu masz źle
	4		4

zef: Czemu tu jest źle ? Skorzystałem ze wzoru x=x_o+2kπ lub x=(π−x_o)+2kπ

zef: Wszystko już widzę na wykresie, ale czy ten wzór jak tak jest zły w tym przypadku ?

PW: Nie ma takiego wzoru. Spójrz na wykres https://matematykaszkolna.pl/strona/426.html − interesują nas wartości ujemne na przedziale [0, 2π).

zef: Tutaj znalazłem ten wzór: http://www.matmana6.pl/tablice_matematyczne/liceum/trygonometria/116-rozwiazania_rownan_trygonometrycznych_typu_sinxa_cosxa_tanxa

PW: Niebezpieczne jest korzystanie z takich "kompendiów". Mówią o sytuacji, gdy a >0, tylko tego wyraźnie nie zaznaczyli.

zef: To w jaki sposób najlepiej rozwiązywać takie przykłady ? Jest sposób bez rysowania wykresu ? Jakiś wzór ?

PW: Myślę, że bezpieczniej jest rysować wykresy niż zapamiętywać wzory. Dobrze jest rysować wykresy sinusa i kosinusa na przedziale [−π, π). Przedział ma długość okresu, a więc wszystkie inne rozwiązania różnią się o wielokrotność okresu, natomiast lepiej widać te podstawowe rozwiązania (dla kosinusa symetryczne względem osi OY, dla sinusa

	π		π
symetryczne względem osi x =		− te dodatnie − lub osi x = −		− te ujemne).
	2		2

zef: Dziękuję za wyjaśnienie, jednak bardzo by mi zależało gdyby Mila się wypowiedziała jeśli chodzi o ten wzór.

Adamm:

	7π
przecież wzór jest poprawny, obejmuje wartość
	4

zef: Ale nie wiem czy obejmuje też inne wartości, według odpowiedzi wynik to :

	5π		2
x=		+		kπ
	12		3

	7π		2		−π		2
x=		+		kπ tutaj mi wyszło		+		kπ gdzie k∊C ale chyba i to i to jest
	12		3		12		3

dobre bo te wartości w obu przypadkach dla k∊C będą takie same

Adamm:

−π		2		7π
	+		π=
12		3		12

zef: Adamm Tak dla k=1 będzie się to zgadzało ale jak sprawdzić czy wszystkie wyniki się pokryją ?

Adamm:

	2
różnią się o		π, chyba oczywiste że się pokrywają
	3

zef: Chyba już sam wiem.

	2π
sin3x okres tej funkcji to
	3

−π		2		7π		2
	+		kπ=		+		kπ
12		3		12		3

8π		2π
	=		czyli okres naszej funkcji, wszystko się zgadza, dziękuję Panowie, z tego
12		3

wynika że obie odpowiedzi są dobre.

PW: Tak. Cofam to co napisałem − że nie ma takiego wzoru. Po prostu takie podejście jest sprzeczne z moimi nawykami. Uczyli dziecko: "Weź przedział o długości 2π, np. [0, 2π) i znajdź rozwiązania podstawowe". Tak się przyzwyczaiłem, i jest to sposób dobry, widoczny na wykresie.

Mila:

	1
1)sinx=
	2

	π
x0=
	6

	π		π		5π
x1=		+2kπ lub x2=π−		+2kπ⇔x2=		+2kπ
	6		6		6

	1
2) sinx=−
	2

	5π
x1=x0+π+2kπ lub x2=		+π+2kπ
	6

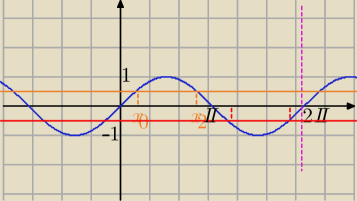
[przesunięcie poprzednich rozwiązań o π, ja tak rozwiązuję w przedziale <0,2π> ] albo można x₂=2π−x₀ patrz wykres i czerwoną linię, tak podał PW

	7π		11π
x=		+2kπ lub x=		+2kπ
	6		6

Teraz spróbuj swój przykład rozwiązać.

zef: Milu dziękuję za wytłumaczenie Swój przykład rozwiązałem korzystając z gotowego wzoru, bo i ze wzoru i sposobem PW wychodzi dobry wynik

Mila: