Pomocy
Ola98: Trapez prostokątny o wysokości 2 cm dłuższej podstawie równej 5 cm i kącie
ostrym o mierze 45 stopni obraca się dookoła prostej zawierającej krótszą podstawę.
Oblicz objętość otrzymanej w ten sposób bryły
5 lis 20:02
Jack:
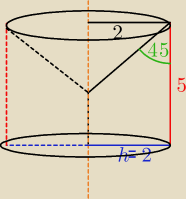
5 lis 20:21
Ola98: A jak obliczyć?
5 lis 20:22
Jack:
Vbryły = Vwalca − Vstożka
5 lis 20:26
Ola98: A jak wartości podstawic?
5 lis 20:29
Eta:
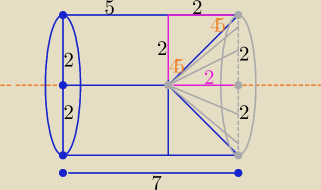
Taką bryłą jest walec z wydrążonym po prawej stronie stożkiem
wymiary walca : H= 7 , r= 2
wymiary stożka : h=2 i r=2
V(bryły) = V(walca ) − V(stożka
V(bryły )= πr
2(H −(1/3)h) = ........
podstaw dane i po b
ólu

5 lis 20:29
5 lis 20:32
Jack:
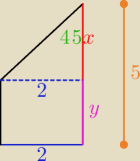
wzory chyba znasz.
wzor ogolny :
u nas : r = 2, h = ?
H znajdziemy, wiec ze kat ostry w trapezie ma 45 stopni.
co do tego h(patrz rysunek)
x = 2
zatem H = 2
czyli podsumowujac
wzor ogolny :
V
walca = π r
2 h,
u nas : r = 2, h = 5
czyli
V
walca = π * 4 * 5
5 lis 20:36
Ola98: To dane mam podstawic i pod V bryły walca i stożka? Czy po prostu podstawic co podałeś?
5 lis 20:36
Eta:

5 lis 20:37
Jack: w stozku wszedzie duze H mialo byc w danych...ehh
5 lis 20:37
Eta:
"krótka piłka"

V= πr
2( H
w−(1/3)h
st)=.....
5 lis 20:39
Ola98: | | 1 | |
Tylko mam w odpowiedzi ze powinno wyjść 17 |
| |
| | 3 | |
5 lis 20:41
5 lis 20:43
Jack: no i tyle wyjdzie.
5 lis 20:47
Eta:
Na rysunku pomyłkowo oznaczyłam
Ma być:
H=5 h=2 i r=2
| | 1 | |
V= π*4(5−(2/3))= 17 |
| π |
| | 3 | |
5 lis 20:47
Ola98: A skąd jest te 2/3?
5 lis 20:52
Ola98: Już wiem
5 lis 20:53
Eta:

5 lis 20:54
Ola98: Dziękuję Eta


5 lis 20:56
Jack: Moje rozwiazanie sie nie podoba, no trudno...
5 lis 21:50
Eta:
Łap
Jack ....

5 lis 22:28

 Taką bryłą jest walec z wydrążonym po prawej stronie stożkiem
wymiary walca : H= 7 , r= 2
wymiary stożka : h=2 i r=2
V(bryły) = V(walca ) − V(stożka
V(bryły )= πr2(H −(1/3)h) = ........
podstaw dane i po bólu
Taką bryłą jest walec z wydrążonym po prawej stronie stożkiem
wymiary walca : H= 7 , r= 2
wymiary stożka : h=2 i r=2
V(bryły) = V(walca ) − V(stożka
V(bryły )= πr2(H −(1/3)h) = ........
podstaw dane i po bólu

 Przeczytaj ostatni wpis .https://matematykaszkolna.pl/forum/335183.html To juz naprawde rece opadaja
Przeczytaj ostatni wpis .https://matematykaszkolna.pl/forum/335183.html To juz naprawde rece opadaja 
 wzory chyba znasz.
wzor ogolny :
wzory chyba znasz.
wzor ogolny :

 V= πr2( Hw−(1/3)hst)=.....
V= πr2( Hw−(1/3)hst)=.....



