okrag opisany na trojkacie wojt: oblicz promien okregu opisanego na rownoramiennym trojkacie prostokatnym ktorego obwod jest rowny 4

wojt: skąd tam się wziął √3?

wojt: R= U{4}}{2+2√2}

	4
Na innej stronie znaazłem takie przekształcenie R=		⇒2(2−2√2) mógł(a)by mi
	2+2√2

Pan/Pani powiedzieć dlaczego tak się dzieje? albo powiedzieć jak to się nazywa to bym poszukał wyjaśnienia na własną rękę

wojt: proszę o pomoc

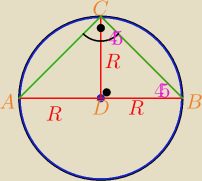Jack: Polowa trojkata ABC to trojkat DBC. Trojkat DBC jest rownoramienny, bo ma dwa boki dlugosci R, skoro jest to trojkat rownoramienny i na dodatek prostokatny, no to katy w nim maja po 45^o,45^o,90^o zatem dlugosc BC to inaczej przekatna kwadratu o boku R, zatem R√2 (to wynika tez z tego jakbysmy zrobili sinus, albo cosinus kata 45) Zatem obwod calego trojkata ABC to 2R(podstawa trojkata) + 2*R√2(ramiona trojkata) wiemy ze ten obwod wynosi 4. zatem 2R + 2R√2 = 4 /:2 R + R√2 = 2 R(1+√2) = 2

	2
R =
	1+√2

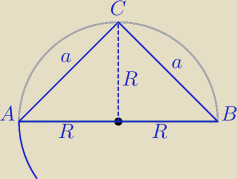Mila: a=R√2 obw=2a+2R 2*R√2+2R=4 /:2 R√2+R=2 R*(√2+1)=2 /*(√2−1) R*(2−1)=2(√2−1) R=2*(√2−1) =========

Mila: Ja wiedziałam, że uderzyłaś w inny klawisz. Wszyscy wiemy, że umiesz wszystko.

wojt:

	2
Bardzo dziękuję za dokładne wyjaśnienie, a R=		można jakoś zamienić na 2(√2−1)
	1+√2

bo tak mam w odpowiedziach, mógłby Pan mi powiedzieć jak się nazywa ta zasada? bo nie znam metody takiego zamieniania, czy to jest po prostu na logikę?

wojt: okej dziękuje

Eta: https://matematykaszkolna.pl/strona/1635.html