trapez Konrad: W trapezie ABCD (AB ∥CD) podstawa AB tworzy z przekątną AC kąt dwa razy mniejszy niż z ramieniem BC. Wiedząc ,że |AB|=23 ,|BC|=9 oraz pole trapezu jest równe 60√2 Oblicz długości pozostałych boków tego trapezu. Pomoże m ktoś bo siedzę nad tym zadaniem już 4 godziny i nic byłbym bardzo wdzięczny za pomoc

Mila: Policzyłam. Masz odpowiedź? Jeśli się zgadza z moimi wynikami, to napiszę .

Eta: |CD|=7 i |AD|=√113

Mila: Tak mam Eto. Korzystałaś z sin(3α)?

Eta: tak

Mila:

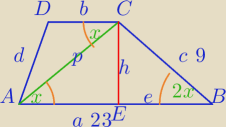
23+b
	*h=60√2⇔(23+b)*h=120√2
2

∡ACB=180−3x W ΔABC:

23		9
	=		, sinx>0⇔
sin(180−3x)		sinx

23		9
	=		⇔
sin(3x)		sinx

23		9		23		9
	=		⇔		=
3sinx−4sin3x		sinx		3−4sin2x		1

stąd

	1		√8
sinx=		z jedynki tryg. cosx=
	3		3

	1		2√2
2sinx*cosx=sin2x=2*		*
	3		3

	4√2
sin(2x)=
	9

W ΔCEB:

	h
sin(2x)=
	9

h		4√2
	=		⇔h=4√2
9		9

(23+b)*h=120√2⇔(23+b)*4√2=120√2 23+b=30 b=|CD|=7 dalej poradzisz sobie? Może Eta ma inny sposób, to na pewno napisze.

Eta: Mam tak samo

Mila: Dziękuję Eto za odpowiedź .

Eta: Szkoda,że zainteresowani milczą ! I właśnie to mnie zniechęca .......

Ajtek: Dobry wieczór Eta, Mila Tutaj jest chętny 334487

Eta: Witaj Ajtek