Pochodne Jack: jak sie robi pochodna funkcji wykladniczej i logarytmicznej? np. y = 2^x albo y = 3^2x i logarytmiczne np y = log₂x albo y = log₁₀x² i inne

Adamm: wykładnicze sprowadzasz to postaci e^x tzn. 2^x=e^ln2x i funkcja złożona logarytmiczne podobnie

Janek191: y = 2^x y ' = 2^x *ln 2 −−−−−−−−−− y = 3^2x = 9^x y ' = 9^x*ln 9 −−−−−−−−−−−

Adamm: np. y=2^x=e^xln2 y'=ln2*e^xln2=2^xln2

	lnx
y=log2x=		=
	ln2

	1
y'=
	xln2

Jack: Adamm oki, ale nie wiem jak zrobic pochodna z funkcji e^ln2x chyba ze to tak dziala ze to jest ln2x * e^{ln2x − 1}

Jack: Janek, jak Ty to... ?

Leszek: Najlepiej zamienic na funkcje logarytmiczna ln np y=2^x czyli ln y = ln(2^x) zatem ln y = x*ln 2 Czyli y =e^{x*ln 2} Wowczas pochodna y ' = e^{x*ln 2}*ln 2 = 2^x*ln 2 i.t.d

Adamm: może nie wiesz więc powiem y=e^x y'=e^x y=lnx

	1
y'=
	x

wyprowadzić też ci mogę ale to już jak chcesz

Adamm: znasz pochodną f. złożonej

Adamm: jak masz f(y) gdzie f jest funkcją x oraz y=g(x) to (f(y))'=f'(y)*g'(x)

myszka: Jack jak chcesz to mogę Ci "zrobić" na szydełku te pochodne

Mila: Jack Masz to we wzorach: 1) (a^x)'=a^xln(a), a>0, a≠1 2) (a^mx)'=m*a^mxln(a) , a>0, a≠1

	1
3)( ln(x))'=		, x>0
	x

4)

	1
(loga(x))'=		, a>0, a≠1, x>0
	xlna

myszka: https://matematykaszkolna.pl/strona/359.html

Jack: Adamm znam pochodna zlozona, tylko na wykladniczej nie wiem co sie dzieje Obejdzie sie bez wyprowadzania (chyba ) Dziekuje wszystkim !

Adamm: jak opanujesz funkcję złożoną to nie musisz pamiętać wszystkich tych wzorów mi wystarcza xⁿ, e^x, lnx, trygonometryczne, cyklometryczne i własności pochodnych

Saizou : myszka dlaczego porzuciłaś swój uroczy 3−lietrowy nick ?

Leszek: Jezeli student chce nauczyc sie dobrze matematyki powinien umiec wyprowadzac poszczegolne wzoru ,a nie uczyc sie ich na pamiec i korzystac z nich automatyczne. Na dobrych uczelniach daje sie zadania ,aby napodstawie okreslonych definicji wyprowadzac wzory i obliczenia. Ot przyklad Na podstawie definicji prosze wyznaczyc pochodna funkcji f(x)= √x²+1

Jack: nie mialem za bardzo wyprowadzania na podstawie definicji... f(x) = √x²+1

	1
f ' (x) =		* 2x
	2√x2+1

Leszek: A jaka to szkola?

Jack: jestem na 1−wszym roku studiow z informatyki

Adamm:

	f(x+h)−f(x)
limh→0
	h

Adamm: z definicji pochodnej Jack

Jack: bo tak mam maciu

Leszek: To na tym kierunku powinny byc urzywane definicje i dowody twierdzen matematycznych Dobrym podrecznikiem jest Matematyka W.Zakowski i inni . Jest tam spora dowodow przedstawionych w przystepny dla studenta sposob,warto sie z tym zapoznac.

myszka: Hej Saizou Kiedyś na tym forum Wszyscy byliśmy jak w rodzinie Można było podzielić się wiedzą, pożartować nawet do rana A teraz .... wszyscy się obrażają , popisują ....... ( brak słów) Postanowiłam zostać tu szarą myszką ( i nie wiem czy na długo) bo szkoda mi zdrowia Ot to Pozdrawiam

Jack: no to biore funkcje f(x) = x²+1

	x2+1+h − (x2+1)		h
lim		= lim		= ?
	h		h

h→0 chyba cos zle robie...

Adamm: f(x+h), ty wstawiłeś f(x)+h

Jack: aaa no tak

Leszek: Jack to nie ta funkcja ,chdzilo mi o funkcje postaci f(x)=√x²+1

Jack:

	(x+h)2+1 − (x2+1)		2hx + h2
... = lim		= lim		= lim U{2x+h} = 2x?
	h		h

Jack: Leszek wiem, ale z definicji to chyba pierwszy raz w zyciu robie, to nie chcialem sie od razu rzucac

Adamm: tak, dobrze Jack teraz spróbuj funkcję Leszka

Leszek: OK malymi krokami dojdzie dalej Kosmonalta amerykanski na Ksiezycu zrobil maly niesmialy krok ,a ludzkosc zrobila olbrzymi krok .Tak trzymaj

Jack: to na szybko bo mi sie placek spali f(x) = √x²+1

	√(x+h)2 + 1 − √x2 − 1
lim		= dobre pytanie
	h

jednak na szybko nie dam rady, zw ;x

Saizou : Szara myszko wiem o czym mówisz, forum się trochę zmieniło, a raczej użytkownicy. Niestety, smuto jest to co się tutaj dzieje, ale ludzi nie jest tak łatwo zmienić i w 100 % się z Tobą zgadzam Również pozdrawiam (bo to myszka jabłkożerna ) pomnóż przez licznik ze zmienionym znakiem

Mila: Taką granicę liczyłeś nie jeden raz, do dzieła.

Mila: Eta, jesteś gwiazdą na tym forum i wracaj do swojego nicka. Nazwa gwiazdy Ettanin ( Etanim i Etamin), wywodzi się od arabskiego Al Rās al Tinnīn i oznacza głowę smoka.

Jack:

	(x+h)2 + 1 − (x2−1)
... = lim		=
	h(√(x+h)2+1 + √x2−1)

	2hx + h2 + 2
= lim
	h√(x+h)2+1 + h√x2−1

hmm

5-latek : Maciu nie pochlebiaj sobie az tak . Jack zobacz czy dostales emalia ode mnie

Saizou : Jack coś ze znakami masz nie tak jak być powinno

Saizou : Kurcze, literki pomieszałem, miło być Jack a nie Jack

Jack: Krzysiutak, dostalem, dzieki

Jack: oj maciu maciu... Saizou, co jest nie tak?

5-latek : To sie cieszse . Wyslalem tez to samo Metisowi przy okazji Moze zobaczy

Saizou :

√(x+h)2+1−√x2+1		(x+h)2+1−(x2+1)
	=		=
h		h(√(x+h)2+1+√x2+1)

x2+2xh+h2+1−x2−1
	=
h(√(x+h)2+1+√x2+1)

2xh+h2
h(√(x+h)2+1+√x2+1)

Jack: a faktycznie, tam + zamiast −

Jack:

	2x + h		2x		x
... = lim		=		=
	√(x+h)2+1 + √x2+1)		2√x2+1		√x2+1

Saizou :

Leszek: OK tylko za kazdym razem niestety trzeba pisac lim i dopiero na koncu mozna to opuscic gdy podstawiamy h→0

Jack: bo mam np. obliczyc pochodna funkcji y = 4^x arctg x

	1
y' = 4x ln4*arctgx + 4x *
	x2+1

swoja droga, arcusy tez sie wyznacza z definicji?

Leszek: Tak jako funkcje odwrotna do tgx lub sinx i.t.d

Mila: Każdą pochodną możesz z definicji, ale masz wzory to korzystaj w zadaniach. W LO powinieneś mieć to na lekcjach dla prostych funkcji. Czy na wykładach i ćwiczeniach masz pochodne, czy też sam to przerabiasz dla siebie.

Jack: to wezmy funkcje y = arc sinx z def.

	arcsin(x+h) − arcsinx
y ' = lim		= no tu juz naprawde nie wiem co
	h

Jack: Milu mialem pochodne te proste w LO, natomiast na studiach to mielismy pierwszy z 2 cwiczen z tego (bo drugie cwiczenia to obliczanie ekstremow) i do kazdych cwiczen jest kilkanascie zadan z krysickiego zadane wiec jak zaczalem robic to nagle arcusy i wykladnicza. Jednakze sprawdzajac zadanie probne do kolokwium to one sa naprawde straszne

Jack: np pochodna z funkcji

	cosh x		x		1−x2
f(x) =		− ln(ctgh		) + arcsin
	sinh2 x		2		1+x2

Benny: To tylko tak strasznie wygląda, a liczy się bardzo prosto

Jack: znaczy wiem ze h to chodzi o hiperboliczny ale nie mam zielonego pojecia jak to dziala.

Benny: Jak co działa?

Jack: no cokolwiek. Jak to wyglada np. taki sinh, jak sie oblicza jego pochodna. No nie mam zielonego pojecia

Jack: czy na to sa wzory?

Leszek: Jack Tak jak napisalem wykorzystaj metode obliczania pochodnej funkcji odwrotnej

myszka: Dzięki Mila

Jack: Leszku a jak sie oblicza metoda funkcji odwrotnej?

jc: Jack, mniej wysiłku kosztuje udowodnienie ogólnych reguł i potem ich stosowanie.

Adamm:

	ex−e−x
sinh(x)=
	2

jeśli chodzi o wzory to sinh'(x)=cosh(x) cosh'(x)=sinh(x)

	1
tgh'(x)=
	cosh2(x)

	−1
ctgh'(x)=
	sinh2(x)

Jack: straszne rzeczy ja tu widze... dobra , nie bylo pytania

Adamm: Jack weź y=arcsinx wtedy siny=sin(arcsinx)=x

Mila:

Mila: Jack, weź Krysickiego i licz po kolei, tam jest stopniowanie trudności, najpierw proste, potem złożone. Musisz wzory podstawowe opanować. Zasady znasz , nie rzucaj się od razu na bardzo złożone funkcje.

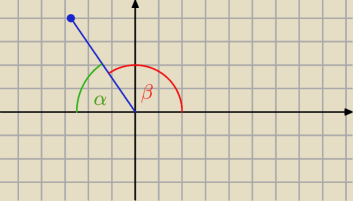
Jack: Jeszcze mam jedno pytanko (kompletnie nie zwiazane z tym co teraz sie dzialo ) jak interpretowac to? puu.sh/rK90D/22ae7be711.jpg oznacza ze kat alfa jest rozwarty czy to jest ten ostry

Jack: Miluok, bede robic "po kolei"

Mila: Masz linka do tej listy na kolokwium.?

Saizou : zakłada się że ramie początkowe to dodatnia półoś X, wiec na ramieniu końcowym leży dany punkt

Jack: Saizou, ale to bedzie jak w koncu Milu mozna powiedziec, ze mam (to raczej sprawdzian niz kolokwium) ale nie chcialbym wszedzie tego udostepniac ; /

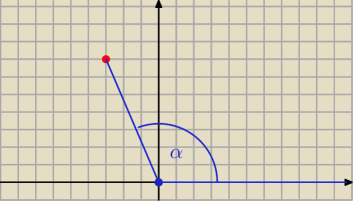
Saizou : chodzi o ten kąt

Jack: no to zeby wyznaczyc funkcje tego kata to akurat biore ten drugi w sensie cos α = − cos (180−α)

Jack: w kazdym razie dzieki !

5-latek : x=−3 y=7 r= √(−3)²+7²= √9+49= √58

	x
cosα=		podsatw i policz
	r

	y
tgα=		podstaw i policz
	x

5-latek :

	y		x
sinα=		i ctgα=
	r		y