okrąg trójkąt op10: Wykaż, że jeżeli promień okręgu opisanego na trójkącie równoramiennym jest dwa razy dłuższy od promienia okręgu wpisanego w ten trójkąt, to trójkąt ten jest równoboczny.

op10: Mam zrobić rysunek? I dopiero wtedy wypisać założenia?

op10: Kompletnie nie wiem jak się zabrać, chyba muszę zrobić rysunek bo inaczej ciężko będzie wypisać założenia

op10:

Jerzy: Dobrze

op10: R; prom. okr. opisanego na trójkącie r; prom. okr. wpisanego w trójkąt R=2r ten Δ jest równoramienny

op10: napisałem tak bo nie wiem jak podpisać wierzchołki na rysunku

op10: Jakieś wskazówki może....?

op10: OK dzięki cześć

op10: Ktoś pomoże

op10: Może mi ktoś pomóc bo ja tego nie potrafię. Nie mam pomysłu.

5-latek: Skoro Jerzy sie zobowiazal pomoc to powinien sie wywiazac z obietnicy ja osobiscie bym z gęby cholewy nie robil

op10: A Ty mógłbyś mi pomóc? Jakieś wskazówki? Proszę, bardzo potrzebuję pomocy..

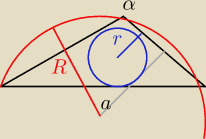
g: W trójkącie równobocznym R/r = 2. Jeśli teraz ten trójkąt zdeformujemy w ten sposób, że jego podstawa o długości 'a' pozostanie w miejscu, ale wierzchołek przesuniemy tak, że kąt α (przeciwległy do podstawy 'a') będzie większy niż 60^o i jednocześnie będzie największym kątem trójkąta, to R się zwiększy i r się zmniejszy, czyli stosunek R/r się zwiększy. Stosując taką deformację można uzyskać trójkąt o dowolnych kątach. Wniosek stąd taki, że R/r = 2 tylko w trójkącie równobocznym i jest to wartość najmniejsza z możliwych.

g: Poprawka. To nie prawda. Początkowo promień R się zmniejszy. Jeszcze pomyślę.

Rafał: a,b,c − długości boków R − długość promienia okręgu opisanego r − długość promienia okręgu wpisanego p − połowa obwodu S − pole trójkąta

	abc		S		abc
Zachodzą związki S=pr i S=		, zatem r=		i R=		. Wykażemy, że w dowolnym
	4R		p		4S

trójkącie R≥2r, przy czym równość zachodzi tylko wtedy, gdy trójkąt jest równoboczny. Istnieją takie dodatnie x, y, z, że a=x+y, b=y+z, c=z+x. Z równości p=x+y+z i wzoru Herona mamy S=√p(p−a)(p−b)(p−c)=√(x+y+z)xyz. Jednocześnie abc=(x+y)(y+z)(z+x).

	abc		2S
Wracając do nierówności,		≥		, czyli abc*p≥8S2. Po podstawieniu powyższych
	4S		p

zależności mamy (x+y)(y+z)(z+x)(x+y+z)≥8(x+y+z)xyz, po podzieleniu stronami przez (x+y+z): (x+y)(y+z)(z+x)≥8xyz. Na mocy nierówności między średnią arytmetyczną i geometryczną: (x+y)(y+z)(z+x)=(xy+xz+y²+yz)(z+x)=xyz+xz²+y²z+yz²+x²y+x²z+xy²+xyz≥8⁸√x⁸y⁸z⁸=8xyz. Równość zachodzi tylko wtedy, gdy wszystkie składniki lewej strony są równe, czyli x=y=z, a w konsekwencji a=b=c.

Rafał: To jest odpowiedź do problemu uogólnionego: Wykazać, że dowolnym trójkącie stosunek długości promienia okręgu opisanego do długości promienia okręgu wpisanego jest większy lub równy 2.

Rafał: Nierówność (x+y)(y+z)(z+x)≥8xyz można wykazać prościej. x+y≥2√xy y+z≥2√yz z+x≥2√zx Po wymnożeniu...

Rafał: O podstawieniu a=x+y, b=y+z, c=z+x więcej tutaj:http://www.deltami.edu.pl/temat/matematyka/geometria/planimetria/2016/05/27/1606delta-deltoid.pdf

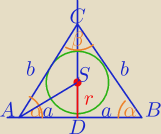
Mila: Środek okręgu wpisanego w trójkąt leży na przecięciu dwusiecznych kątów wewnętrznych trójkąta. R− promień okręgu opisanego r=2r 1) β=180−2α, α− kąt ostry W ΔABC:

2a		2a		a
	=2R⇔		=4r⇔r=
sin(180−2α		sin(2α)		2sin(2α)

W ΔADC:

	α		r		α
tg		=		⇔r=a*tg
	2		a		2

−−−−−−−−−−−⇔

	α		a
a*tg		=
	2		2sin(2α)

	α		1
tg		=
	2		2sin(2α)

α   sin   2		1
	=		⇔
α   cos   2		4sinα*cosα

α   sin   2		1
	=		⇔
α   cos   2		α   α   8*sin *cos *cosα   2   2

	α		1		α
sin		=		⇔ 8sin2		*cosα=1⇔
	2		α   8*sin *cosα   2		2

	1−cosα		1
8*		*cosα=1 ⇔(1−cosα)*cosα=		⇔
	2		4

	1
cos2α−cosα+		=0⇔
	4

	1
(cosα−		)2=0
	2

	1		π
cosα=		⇔α=
	2		3

	π
β=		⇔
	3

ΔABC− Δrównoboczny ================

myszka: Można wykazać twierdzenie odwrotne i po sprawie

Mila: ?

myszka: Mila dlaczego dałaś ? (p⇒q ∧ q⇒p)⇔(p⇔q)

myszka: https://matematykaszkolna.pl/forum/280129.html Tu też Bogdan podał dowód twierdzenia odwrotnego

Mila: Po prostu ciekawa jestem Twojego rozwiązania.

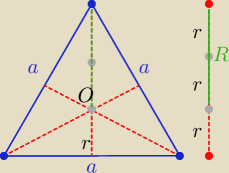myszka: Mila żartujesz?