Ostrosłup Qwadrat: W ostrosłupie prawidłowym trójkątnym kąt płaski przy wierzchołku ma miarę α. Oblicz cosinus kąta zawartego między dwoma sąsiednimi ścianami bocznymi tego ostrosłupa, jeśli:

	7
a) cosα =
	25

Znalazłem tutaj rozwiązanie (https://matematykaszkolna.pl/forum/266564.html ), ale nie ma tu rysunków, więc koniec końców nie wiem z czego wynika część rzeczy.

Mila: Jeśli masz odpowiedź to podaj. Zaraz narysuję.

Qwadrat: Zatem cytuję wpis Bogdana z podanego tematu: c = bsinα ⇒ c² = b²sin²α = b²(1 − cos²α) = b²(1 − cosα)(1 + cosα) Z twierdzenia cosinusów: a² = 2b² − 2b²cosα i a² = 2c² − 2c²cosβ 2b²(1 − cosα) = b²(1 − cosα)(1 + cosα)(1 − cosβ) Po uproszczeniu przez 2b²(1 − cosα): 1 = (1 + cosα)(1 − cosβ)

	1		1		cosα
1 − cosβ =		⇒ cosβ = 1 −		=
	1+cosα		1+cosα		1+cosα

	7		7     25		25		7
dla cosα =		mamy cosβ =		*		=
	25		7   1+   25		25		32

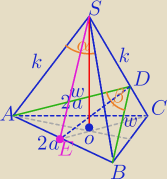
Mila: |AB|=|BC|=|AC|=2a |BD|=|AD|=w, BD⊥AC, AD⊥AC W ΔAES:

	α		|ES|
cos		=
	2		k

	α
|ES|=k*cos
	2

|ED|⊥k

	1		α
PΔABS=		*2a*|ES|=a*k*cos
	2		2

	1
PΔABS=PΔBCS=		k*w
	2

1		α
	k*w=a*k*cos
2		2

	α
w=2acos
	2

W ΔABD z tw. cosinusów: |AB|²=w²+w²−2*w*w*cosβ 4a²=2w²*(1−cosβ)

	4a2
1−cosβ=
	2w2

	4a2		1
1−cosβ=		⇔1−cosβ=
	α   2*(2acos )2   2		α   2cos2   2

	1
cosβ=1−
	α   2cos2   2

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	α
cosα=2cos2		−1
	2

	α
cosα+1=2cos2
	2

	α		7		32
2cos2		=		+1=
	2		25		25

	1		25
cosβ=1−		=1−
	32   25		32

	7
cosβ=
	32

=========================

Qwadrat: Bardzo dziękuję Mila, a czy mogłabyś powiedzieć mi jeszcze z czego wynika:

	α
cosα=2cos2		−1 ?
	2

Antonni: cos2α= cos²α−sin²α cos2α= cos²α−(1−cos²α) cos2α= cos²α+cos²α−1 cos2α= 2cosα−1

	α
to cosα= 2cos		−1
	2

============================

Mila:

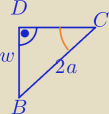
Mila: Można jeszcze innym sposobem : ( bez porównania pól)

	α
∡BCD=(180−α):2=90−
	2

w ΔBCD:

	w
sin∡BCD=
	2a

	α		α
sin∡BCD=sin(90−		)=cos
	2		2

	α		w
cos		=
	2		2a

	α
w=2a*cos
	2

dalej z tw. cosinusów

Qwadrat: Ok, teraz to rozumiem. Bardzo Wam dziękuję

Mila: