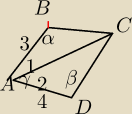
Twierdzenie sinusow i cosinusow Matmaaa: Proszę o pomoc Boki czworokąta ABCD mają długości AB=3,BC=√19, CD=√21, AD=4. Przekątna AC tego czworokąta ma długość 5. Oblicz długość przekątnej Bd

Jolanta: 5²=3²+√19²−2*3*√19*cosα 25=28−6*√19cosα

	1
cosα=
	2√19

	1		75		5√3
sinα=√1−cos2α=P{1−		}=√		=
	4*19		76		2√19

5²=√21+4²−2*4*√21cosβ 8√21cosβ=12

	3
cosβ=
	2√21

	9		5√3
sinβ=√1−cos2β=√1−		=
	4*21		2√21

1 i 2 to kątyγ₁ i₂

5		√19
	=
sinα		sinγ1

	5√3*√19		√3
sinγ1=		=		γ1=600
	2√19*5		2

√21		5
	}=
sinγ2		sinβ

	5		1		1		1
sinγ2=√21*		*		*		=		*√3 γ2=600
	2		√7		5		2

γ=120⁰ AD²=3²+4²−2*3*4cos120⁰

Jolanta: BD²=25−24*cos(90⁰+30⁰) BD²=25−24*(−sin30⁰)=25+12 BD=√37

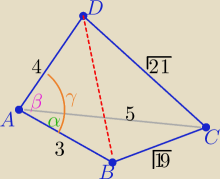
myszka: z twierdzenia kosinusów w trójkątach:

	32+52−19		1
ABC : cosα=		=		⇒ α= 60o
	2*3*5		2

	52+42−21		1
ADC : cosβ=		=		⇒β= 60o
	2*5*4		2

	1
to γ=120o to cos120o=−
	2

z twierdzenia kosinusów w ΔABD: |BD|²= 3²+4²−2*3*4*cos120^o |BD|²= 25+12 =37 |BD|= √37

Janek191: Myszka, jak zawsze, pięknie

myszka:

Jack: pierwszy raz widze, zeby ktos cosinusy pisal przez k

myszka: cosα ( słownie kosinus α ... a nie cosinus α

myszka: Z twierdzenia Carnota

jc: ja tak piszę

myszka: https://matematykaszkolna.pl/forum/290379.html Stara "dobra szkoła"

Jolanta: Jak to robisz że tak ładnie rysujesz.mi te linie ruszają sie i nie moge nad nimi zapanowac

Metis: "stara szkoła" ?

myszka:

Jolanta:

Janek191: Odnośnie kosinusa ( cosinusa) 1) Słownik ortograficzny języka polskiego PWN W − wa 1986 s. 264 jest: cosinus zobacz kosinus cosinusoida zobacz kosinusoida s. 417 jest: kosinus −a, −sie ( skrót : cos ) 2) Słownik ortograficzny PWN W−wa 2005 s. 96 jest: cosinus −sa, − sie ; − sy, −sów zobacz kosinus s.297 jest kosinus −sa, −sie; − sy, − sów skrót : cos W obu słownikach wyraz zobacz odsyła do form zalecanych ( spolszczonych ).