Filip : W ostrosłupie prawidłowym czworokątnym pole podstawy jest dwa razy większe od pola ściany bocznej. Oblicz cosinus kąta α zawartego między sąsiednimi ścianami bocznymi tego ostrosłupa

Bogdan:

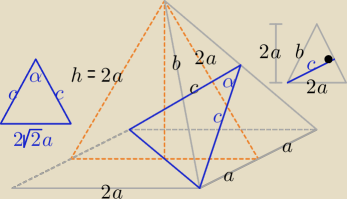
	1
wysokość ściany bocznej h: 2*		*2a*h = 4a2 ⇒ h = 2a
	2

krawędź boczna ma długość b = √4a² + a² = a√5 odcinek o długości c to wysokość ściany bocznej opadająca na krawędź boczną o długości b

	1		1		4a
Z pola ściany bocznej:		*2a*2a =		*a√5*c ⇒ c =
	2		2		√5

	2c2 − 8a2
Na podstawie twierdzenia kosinusów: cosα =		= ...
	2c2