wytłumacz Funkcje: Hejka ludzie pomóżcie i wytłumaczcie! Punkt A i B należą do wykresu funkcji liniowej. Podaj wzór tej funkcji jeśli: a) A(0,0) B(2, −8) b)A (0,5) B(1,3) c) A(3,0) B(0,−7) d) A(−4,0) B(−6,−1) Prosze o wytłumaczenie dwóch pierwszych[ lub wszystkie jesli ktoś zrobi] reszte zrobie sama

Benny: https://matematykaszkolna.pl/strona/1223.html lub A=(x_a,y_a) B=(x_b,y_b) f(x)=ax+b, więc

⎧	ya=axa+b
⎩	yb=axb+b

Adamm: ok a) A(0,0) B(2, −8) oznaczmy tą funkcję f(x)=ax+b (ponieważ jest liniowa) f(0)=0 f(2)=−8 f(0)=a*0+b=b=0 więc b=0 f(2)=2a=−8 a=−4 f(x)=−4x

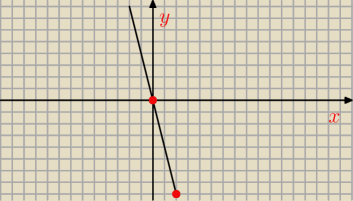
zef: Wytłumaczę najlepiej jak potrafię: Na rysunku jest podpunkt A z zaznaczonymi tymi punktami A(x,y) i B(x,y) Tworzysz z tego układ równań ze względu na to że oba punkty należą do tej prostej: wzór: y=ax+b podstawiasz najpierw punkt A 0=0*a+b później B −8=2a+b i masz układ, który należy rozwiązać wyznaczając a i b 0=0*a+b −8=2a+b

Funkcje: Nie wiem czy wyszedł mi dobry wzór w pierwszym wyszło y= −4 good

Funkcje: znaczy x=−4x [iksa zapomniałam ]

Benny: Z tego układu równań możemy wyprowadzić sobie wzór na prostą. Wyznaczmy z obu równań b. Dostajemy: y_b−ax_b=y_a−ax_a y_b−y_a=a(x_b−x_a)

	yb−ya
a=
	xb−xa

Wstawiamy np. do pierwszego równania wyliczone a i wyliczamy b.

	yb−ya
ya−		*xa=b
	xb−xa

Równanie prostej to y=ax+b, wiec wstawiamy a i b.

	yb−ya		yb−ya
y=		*x+ya−		*xa /*(xb−xa)
	xb−xa		xb−xa

y(x_b−x_a)=(y_b−y_a)*x+y_a(x_b−x_a)−(y_b−y_a)*x_a (x_b−x_a)(y−y_a)=(y_b−y_a)(x−x_b) _________________________________

Funkcje: w pierwszym wychodzi y=−4x?

Funkcje: aa ok

Funkcje: w drugim wychodzi y=−2x+3