równanie A.: (sinx−cosx)(sinx+cosx)=2−k wskaż rozwiązania w zależności od k

Adamm: sin²x−cos²x=2−k 2sin²x−1=2−k 2sin²x−3+k=0

	−3+k		−3+k
(sinx−		)(sinx+		)=0
	2		2

teraz lepiej?

Adamm:

	−3+k
czyli mamy ∞ rozwiązań dla −1≤		≤1
	2

	−3+k		−3+k
i zero rozwiązań dla (−1>		∨		>1)
	2		2

A.: mam w odpowiedzi x=mπ, gdzie m∊C dla k=3 mógłbyś napisać skąd to się bierze?

Adamm:

	−3+k
czyli dla −1≤		≤1
	2

1		5
	≤k/2≤
2		2

1≤k≤5

	−3+k		−3+k
mamy sinx=		∨ sinx=−
	2		2

	−3+k		−3+k		−3+k
x=arcsin(		)+2πn ∨ x=π−arcsin(		)+2πn ∨ x=arcsin(−		)+2πn
	2		2		2

	−3+k
∨ x=π−arcsin(−		)+2πn gdzie n∊Z (całkowite)
	2

dla k∊(−∞;1)u(5;∞) brak rozwiązań

Adamm: ponieważ −1≤sinx≤1

A.: Dziękuję, proszę się nie podszywać.

Iryt: Nie rozkaz, tylko prośba młody kolego. sin²x−cos²x=2−k /*(−1) cos²x−sin²x=k−2 cos(2x)=k−2, −1≤cos(2x)≤1 stąd: −1≤k−2≤1 /+2 1≤k≤3

A.: ja tego nie napisałem, proszę sobie ze mnie nie żartować

Adamm: aha, zaponiałem dać tam pierwiastki, więc moja odpowiedź jest nieprawidłowa

Iryt: Napisz których postów nie pisałeś (podaj godziny).

Adamm: Iryt, podszywająca osoba nie ma kropki

Adamm:

	−3+k
jeśli chodzi o moją odpowiedź, to była by taka sama jak Iryta, jeśli założyłbym że		≤0
	2

A.: Dobrze, to ja autor postu. Przepraszam za kłopot. Podam wam treść zadania: 1. Równanie (sinx−cosx)(sinx+cosx)=2−k: a) nie ma rozwiązań dla k=1 b) ma nieskończenie wiele rozwiązań dla k=1,5 c) ma rozwiązania x=mπ dla k=3 Jedna z tych trzech odpowiedzi jest prawidłowa, mam uzasadnić która. Moje posty: 3 wrz 2016 17:51 3 wrz 2016 18:08 3 wrz 2016 18:16 3 wrz 2016 18:18 + ten

Adamm: sin²(mπ)−cos²(mπ)=1 cos(2mπ)=1 1=1 tożsamość

Adamm: zakładam że m należy do całkowitych

Mila: Dziękuję Adamm, już w porządku?

Adamm: dla b) cos2x=−3 sprzeczność a) ZW=<−1;1>

A.: Dziękuję bardzo za cierpliwość i jeszcze raz przepraszam za kłopot

Mila: Adamie jak to wyszło (−3) w (b) ?

Adamm: chodziło mi dla k=5, zapomniałem wspomnieć

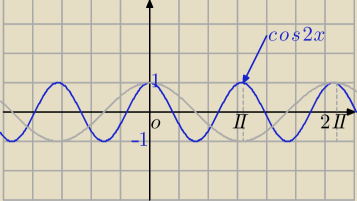
Mila: a) ma rozwiązania dla k=1 bo cos(2x)=k−2⇔cos(2x)=−1

	3
b) k=
	2

	3
cos(2x)=		−2
	2

	1
cos(2x)=−		ma nieskończenie wiele rozwiązań
	2

c) k=3 cos(2x)=k−2 cos(2x)=3−2 cos(2x)=1 2x=0+2mπ⇔x=mπ, m∊C

Mila: Może coś pominąłeś w treści?

A.: Treść jest dokładnie taka jak napisałem, sprawdziłem jeszcze raz. Odpowiedź "a" na pewno odpada. Ale powinna być tylko 1 dobra

Adamm: pomyliłem cosx=k−2 z cosx=2−k a jeśli chodzi o k=1,5 to myślałem że chodzi o to że k=1 lub k=5

Mila: a) odpada, bo równanie ma rozwiązanie , ale w (b) też są rozwiązania, z jakiego to zbioru, może mam.

Mila: Adamie, sprawdź moje rozważania 19:14, może czegoś nie zauważyłam.

Eta: https://matematykaszkolna.pl/forum/329983.html

A.: Eta, a czy mogłabyś powiedzieć czemu odpowiedź b jest niewłaściwa, proszę?

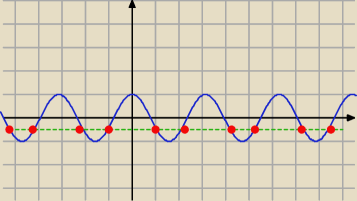
Eta: Odp b) też jest poprawna bo: −cos(2x)= 0,5 ⇒ cos(2x)= −0,5 ma nieskończenie wiele rozwiązań

Eta:

Mila: O, dobrze, że jesteś Eto, Dawno Cię nie widziałam na forum

Eta: Witam , witam

Mila: Odpoczęłaś? Piękne było lato, temperatura w sam raz. Krajobrazy bajecznie zielone, tylko za dużo samochodów na drogach.