trygonometria gość:

	1		1		kπ
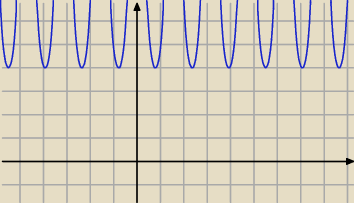
1. Funkcja f(x)=		+		,x∊R−{x:x=		,k∊C}:
	sin2x		cos2x		2

a) jest okresowa b) przyjmuje najmniejszą wartość równą 4 c) nie przyjmuje wartości największej 2. Dla każdej liczby rzeczywistej x prawdziwa jest nierówność: a) cos²x ≥ sinx b) 2sin2x+3cos2x < 3,9; c) sinxcosx > −0,53 Bardzo proszę o pomoc jeszcze w tych dwóch zadaniach. Która odpowiedź i dlaczego jest prawidłowa, oraz dlaczego pozostałe są błędne. Będę bardzo wdzięczny. Wiem, że te zadania pewnie wydają się łatwe, ale naprawdę ich nie rozumiem.

Janek191:

	1		1		sin2 x + cos2 x
f(x) =		+		=		=
	sin2 x		cos2 x		sin2 x* cos2 x

	1		1		4
=		=		=
	sin2 x*cos2 x		0,25*sin2(2x)		sin2 (2x)

y_min = 4

yht: 1.

	1		1		cos2x		sin2x
f(x) =		+		=		+		=
	sin2x		cos2x		sin2x * cos2x		sin2x * cos2x

	cos2x + sin2x		1		1
=		=		=		=
	sin2x * cos2x		sin2x * cos2x		(sinx*cosx)2

	1		1		1
=		=		=		=
	1   ( * 2sinxcosx)2   2		1   ( * sin2x)2   2		1   *sin22x 4

	1		4		4
		= 1 *		=
	sin22x   4		sin22x		sin22x

a) prawda, ale dobrego uzasadnienia (poza rysowaniem wykresu) nie mam. Jeśli uczysz się do matury to zadań z okresowością funkcji na pewno nie będzie (nawet na rozszerzeniu) b) prawda, wystarczy zauważyć że sin²2x przyjmuje (akurat dla tej funkcji) wartości z zakresu

	4
(0,1> zaś funkcja wyrażona jest przez ułamek		którego licznik i mianownik
	sin22x

przyjmują wartości dodatnie dla każdego x należącego do dziedziny funkcji. Stąd wynika, że ułamek (przy stałej wartości licznika) przyjmuje wart. tym mniejszą, im większy jest mianownik

	4
Zatem dla mianownika równego 1 mamy		= 4 i to jest najmniejsza wartość funkcji f(x)
	1

PS. Wyrażenie sin²2x w ogólnym przypadku przyjmuje wartości <0,1> ale tutaj 0 nie może być bo

	4
jest		i wtedy mianownik byłby zerem, stąd (0,1>
	sin22x

c) prawda, zakres wartości (0,1> pokazuje, że sin²2x nie przyjmuje wartości najmniejszej. bo może być 0.01, może być 0,00001 itd. także jeśli nie da się wskazać najmniejszej wartości mianownika, to nie da się też wskazać największej wartości funkcji f(x) zatem f(x) nie przyjmuje wart. największej Zad. 2

	π
a) nieprawda, weźmy x=		.
	2

Wtedy

	π		π
cos2		≥ sin
	2		2

0² ≥ 1² → sprzeczność b) prawda Niech 2x = t Rozpiszmy lewą stronę nierówności 2sint+3cost = 2sint+2cost + cost = 2(sint+cost) + cost =

	π		π
= 2*√2(sint+		) + cost = 2√2(sint+		) + cost
	4		4

	π
wyrażenie (sint+		) przyjmuje wartości z zakresu <−1,1>
	4

	π
wyrażenie 2√2(sint+		) przyjmuje wartości z zakresu <−2√2, 2√2>
	4

przybliżając wartość pierwiastka √2 ≈ 1,41 otrzymujemy zakres <−2,82; 2,82> cost przyjmuje wartości <−1,1>

	π
nawet jeśli przyjmiemy skrajny przypadek że cost oraz 2√2(sint+		) przyjmą
	4

(jednocześnie) największe możliwe wartości

	π
a więc cost=1, oraz 2√2(sint+		) ≈ 2,82, to wtedy
	4

	π
2√2(sint+		) + cost = 3,82
	4

co i tak jest mniejsze od 3,9 c) prawda Rozpiszmy lewą stronę

	1		1
sinxcosx =		* 2sinxcosx =		*sin2x
	2		2

sin2x przyjmuje wartości z zakresu <−1,1>

	1		1		1
zatem		*sin2x przyjmuje wartości z zakresu <−		,		>
	2		2		2

	1		1
nawet jeśli		*sin2x przyjmie najmniejszą możliwą wartość równą −		= −0,5 to i tak
	2		2

ta wartość jest większa od −0,53 −0,5 > −0,53 logiczne więc jest, że każda większa wartość od −0,5 będzie > −0,53

gość: Dziękuję bardzo za odpowiedzi

Adamm: jeśli chodzi o okresowość to korzystając z okresu dla sin oraz cos mamy okres co najmniej równy 2π

Adamm: jeśli chodzi o c)

	4
to dla lim sin22x→0+		= ∞
	sin22x

gość : Ktoś może potrafi uzasadnić 1a?

Adamm: f(x)=f(x+2π) to jest twoje uzasadnienie

Mila: https://matematykaszkolna.pl/forum/330010.html

gość : Mila, dziękuję