q maciu: moze ktos podac linka z zadaniami z nierownosci kwadratowcyh gdy delta=0,i jest 1 mzerowe? tu na tej stronie nie ma takich kompletnia nie pojmuje przedziałów jesli jest 1 mz

5-latek: https://matematykaszkolna.pl/forum/329458.html

maciu: juz czytalem ten temat,nie pojmuje :(

maciu: koniecznie sie musze tego nauczyc dlatego ze akurat nierownosci pojmuje i to na 100% bedzie jako zad 26,ale nie pojmuje przedzialow jak jest jedno miejsce zerowe

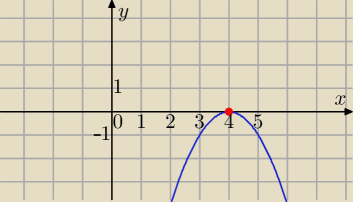
Smule: to tak trudno spojrzec na wykres i wywnioskowac? funkcja ≥ 0 dla każdego x (dla x = 3, wartość = 0, dla innych większa od 0) funkcja > 0 dla każdego x poza 3 (bo dla x = 3 wartość = 0) funkcja ≤ 0 tylko dla x = 3 funkcja < 0 dla żadnego x

Mila: Przykłady: 1) x²−4x+4>0 ( można od razu "zwinąć": x²−4x+4=(x−2)²) albo Δ=16−16=0

	4
x1=x2=		=2
	2

x²−4x+4=(x−2)² parabola skierowana do góry Szkic (x−2)²>0⇔ x<2 lub x>2 Można zapisać tak: x∊R\{2} 2) x²−4x+4≥0 (x−2)²≥0 x∊R

maciu: a teraz narysój proszr jak są inaczej ramiona skierowane ,bo też tak może być,i wszystkie mozliwe schematy

Smule: rozwiaz nierownosc x² + 2x + 1 ≥ 0 x² −2x + 1 < 0

maciu: x<2 lub x>2 Można zapisać tak: x∊R\{2} no to to dotyczy,x<2 czy x>2

maciu: dobra rozwiąze te 2 nierownosci,prosze wszystkich nie robcie tego,ja rozwiaze

maciu: przykład 1 x(−nieskonczonosci do −1 ,−1 do + niekso

Smule: i jeszcze jedna −x² + 8x − 16 > 0

maciu: w drugim podobnie tyle ze nie −1 a 1

Smule: źle

maciu: o o taka mi chodziło 19 01

Smule: masz znak ≥

Smule: oba źle

maciu: ale ja nie wiem jak ten znak zrobić (wiem ze on ma byC) a tak to dobrze?

Smule: dobra przyklad 1 funkcja przyjmuje wartosci wieksze lub rowne 0 dla .. jakiego x?

maciu: jest wieksze =od 0 od (−nieskonczonosci do 0 i plus nieskonczonosci do 0

maciu: od minus nieskonczonosci do 0 i od 0 do plus nieksonczonci

Smule: nie. przecież dla x = −1, wartość równa 0 x należy do liczb rzeczywistych

maciu: −x2 + 8x − 16 > 0 x= 2 x(zbiór pusty?)

Smule: Dobrze a jeśli by było −x² + 8x − 16 ≥ 0 ?

maciu: nalezy od −nies do 0 i od 0 do +nies

maciu: dobrze?

Mila: 1) −x² + 8x − 16 ≥ 0 Δ=0

	−8
x0=		=4
	2*(−1)

−x²+8x−16=−(x−4)² −x² + 8x − 16 ≥ 0⇔ −(x−4)²≥0 parabola skierowana w dół Szkic, Tylko x=4 spełnia tę nierówność 2) −x² + 8x − 16 ≤ 0 x∊R każda liczba spełnia tę nierówność 3) −x² + 8x − 16 < 0 x∊R\{4} albo taki zapis x<4 lub x>4 Możesz też mieć taki zapis na maturze: x∊(−∞,4)∪(4,∞)

maciu: bardzo prosze,taki podobny komentarz 19 22 tylko że ramiona inaczej skierowane ,od tego moze zalezec 30%,bo z zamknietych bedzie 12−13 pkt za nierownosc jest 2, ja umiem nierownosci,ale mam problem jak jest 1 mz,bardzo prosze podobny schemat tylko inaczej ramiona

maciu: bardzo prosze

Eta: 1/ x²−6x+9≤0 2/ x²+4x+4 >0 3/ 2x²−20x+50≥0 4/ x²−8x+16 <0

maciu: naprawde bardzo prosze

maciu: dobra robie nierownosci

maciu: 1. od − nie do 3 od 3 do plus niesk

maciu: w drugim zbior posty

maciu: zad 3 x(−nieskonczonsci do 5,5 + nieskonczonosci

maciu: zad 4 tego nie pojmuje

5-latek: Zadania nr 1 2 3 4 sa to zadnia na wzory skroconego mnozenia Jesli delta =0 to zwijasz do wzoru skroconego mnozenia bo jest pierwistek podwojny i tylko sie sprawdza czy ta nierownosc jest prawdziwa

maciu: nic te wzory nie maja do rzeczy jak delta 0 to trzeba wyliczyc x ,nie pojmuje tych przedziałów

5-latek: x²−6x+9≤0 (x−3)²≤0 ta nierownosc jest prawdziwa tylko dla x=3 A teraz policz delte i wyznacz miejsce zerowe i zobacz czy nie wyjdzie x=3

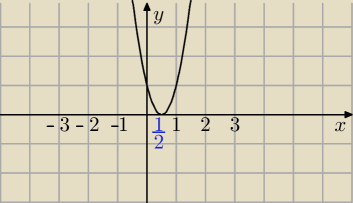
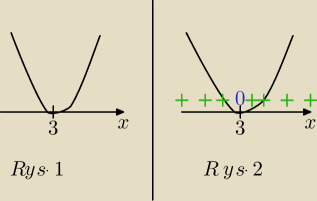
yht: Masz problem z odczytaniem przedziałów.. x∊... Radzę Ci robić to tak: ≤ czyli − (minus) lub 0 (zero) < czyli − (minus) ≥ czyli + (plus) lub 0 (zero) > czyli + (plus) Przykładowo dla nierówności x²−6x+9≤0 wyliczasz sobie deltę, wychodzi Δ=0 potem wyliczasz x₀=3 x²−6x+9, czyli parabola z ramionami w górę, z jednym miejscem zerowym x₀=3 czyli masz wykres taki jak na Rys. 1 Jeśli już jesteś na tym etapie, to tuż nad osią x zaznaczasz sobie: plusy (+) tam, gdzie wykres jest nad osią x zera (0) tam, gdzie na wykresie są miejsca zerowe (wykres styka się z osią x) minusy (−) tam, gdzie wykres jest pod osią x (w nierówności x²−6x+9≤0 akurat minusów nie będzie bo nie ma wykresu pod osią x) masz w ten sposób wykres taki jak na Rys. 2 Teraz patrzysz się na znak nierówności: x²−6x+9 ≤ 0 Piszesz w rozwiązaniu tak: ≤ czyli − (minus) lub 0 (zero) Rozwiązaniem nierówności będą te wszystkie iksy, w których są minusy (−) bądź zera (0) Teraz wystarczy sczytać rozwiązanie z Rys. 2 Minusów w ogóle nie ma, a zero jest tylko dla x=3 Zatem: Odp. Rozwiązaniem nierówności x²−6x+9≤0 jest x=3

maciu: x=3

5-latek: x²+4x+4>0⇒(x+2)²>0 2x²−20x+50≥0 dziele przez 2 x²−10x+25≥0 ⇒(x−5)²≥0 Ostani zrob sam

5-latek: Juz kolega wytlumaczyl

maciu: FE−NO−ME−NAL−NIE yht

Eta: No to jak "fenomenalnie" zrozumiałeś to podaj rozwiązania: 1/ x²< 2x−1 2/ x² −10x ≥ −25 3/ x²+3x≤ −4 −x

Eta: I jeszcze takie: 4/ (x−3)² −4>0 5/ 3x− ( x+1)²≤ 5x −x²

maciu: x²−2x+1<0 x²−10x+25>=0 x²+4x+4<=0

maciu: w czwartm x=3 a co zrobić w 5?

maciu: te 4 i 5 przykłady dziwne jakies

bezendu: x²−2x+1<0 (x+1)²<0 x∊∅ Podstaw sobie obojętnie jaką liczbę to zobaczysz czemu tak. x²−10x+25≥0 (x−5)²≥0 x∊ℛ Obojętnie jaką liczbę podstawisz to zawsze spełni warunek nierówności x²+4x+4≤0 (x+2)²≤0 x=−2

bezendu: a²−b²=(a−b)(a+b) (x−3)²−4>0 (x−3)²−2²>0 (x−3+2)²(x−3−2)²>0 (x−1)(x−5)>0 x∊(−∞,1)∪(5,∞)

maciu: wszystko tylko nie te wzory,bez tego tez mozna rozwiazac nierownosc

maciu: bezendu mozesz zrobic taki wyklad jak Mila w 19 22,wszystko tak samo,tylko,żeby ramiona były inaczej skierowane i do tego te przedziały,bardzo prosze

maciu: zad 5 nie wiem gdzie zrobilem blad w zapisie 3x−x²+2x+1<=5x−x² 5x−x²+1<=5x−x² 6x²+1<=0

maciu: bardzo was prosze

yht: Co do 4/ Musisz wiedzieć jak się liczy wyrażenia typu (x−4)² itp. (x−4)² = (x−4)(x−4) = x² − 4x − 4x + 16 = x² − 8x + 16 (x−6)² = (x−6)(x−6) = x² − 6x − 6x + 36 = x² − 12x + 36 (3x−4)² = (3x−4)(3x−4) = 9x² − 12x − 12x + 16 = 9x² − 24x + 16 (1−5x)² = (1−5x)(1−5x) = 1 − 5x − 5x + 25x² = 25x² − 10x + 1 z plusem w nawiasie jest jeszcze prościej: (3x+4)² = (3x+4)(3x+4) = 9x² + 12x + 12x + 16 = 9x² + 24x + 16 −−−−− Dobrze by było jakbyś wiedział jak się rozpisuje przykłady typu 3(x−5)² 3(x−5)² = 3(x−5)(x−5) = 3(x²−5x−5x+25) = 3(x²−10x+25) = 3x² − 30x + 75 4(x−7)² = 4(x−7)(x−7) = 4(x²−7x−7x+49) = 4(x²−14x+49) = 4x² − 56x + 196 6(4−x)² = 6(4−x)(4−x) = 6(16 − 4x − 4x + x²) = 6(16 − 8x + x²) = 96 − 48x + 6x² 5(6−3x)² = 5(6−3x)(6−3x) = 5(36 − 18x − 18x + 9x²) = 5(36 − 36x + 9x²) = 180 − 180x + 45x² itp. Dla ćwiczenia, rozpisz sobie 3(8−x)². Powinno z tego wyjść 3x² − 48x +192. −−−−−−− Co do 5/ Musisz wiedzieć jak się rozwiązuje przykłady w których pojawia się minus przed nawiasem do kwadratu: −(x−5)² = −(x−5)(x−5) = −(x² − 5x − 5x + 25) = −(x² − 10x + 25) = −x² + 10x − 25 −(x+3)² = −(x+3)(x+3) = −(x² + 3x + 3x + 9) = −(x² + 6x + 9) = −x² −6x − 9 −(3−4x)² = −(3−4x)(3−4x) = −(9 − 12x − 12x + 16x²) = −(9 − 24x + 16x²) = −9 + 24x − 16x²

bezendu: Ale do którego przykładu chcesz ?

maciu: o boże

maciu: bezendu tak samo zrób jak mila w 19 22 tylko,że ramiona inaczej skierowane

maciu: yht,ale to naprawde konieczne? ja chce tylko rozwiazywac nierownosci kwadratowe

yht: mogą dowalić taką nierówność jak Eta podała przykłady 4/ i 5/ i wtedy koniecznie musisz to umieć obliczać żeby rozwiązywać takie nierówności

maciuu: zadanie 4 zapis moj x²−6x+5>0

yht: dobrze ! Teraz delta i moim sposobem rozkminisz

Eta: Nie podszywaj się pod maciu

Eta: maciuu ≠ maciu

maciuu: ale to naprawde maciu

Eta:

maciu: słuchaj yht,wiele mi pomagłeś i dzięki tobie pojmuje pierwiastki,ale jeśli mam być szczery to nie pojmuje,twej metody

Eta: I masz Ci babo placek

maciu: przyrzekam na życie mojej matki,że ja ten przykład zrobiłem

maciu: yht łatwiej byłoby mi pojąć coś w stylu 19 22,jakbyś zrobił podobny schemat,tyle że z ramionami skierowanymi inaczej i opisał różne przypadki bardzo bym prosił

maciu: to daj przykład i zrobie,jak nie wierzysz

yht: To w takim razie rób nierówności tak jak się nauczyłeś wcześniej − proste

maciu: tyle,że ja nie umiem nierównośći,jeśli jest 1 miejsce zerowe

maciu: moglbym pojac 19 22,tylko jeszcze trzeba inaczej ramiona zeby byly i omowione inne przypadki

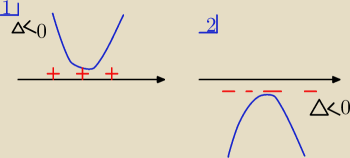
Eta: 1/ ramiona do góry i Δ<0 ( parabola cała nad osią) czyli taka nierówność >0 lub ≥0 dla x∊R <0 −−− piszesz nierówność sprzeczna ( bo paraboli nie ma pod osią 2/ parabola ramionami do dołu i Δ<0 ( parabola cała pod osią ) czyli nierówność ze znakiem >0 lub ≥0 −−− jest sprzeczna zaś ze znakiem <0 to x∊R To były dwa przypadki gdy delta <0 ( ujemna

yht: 1) 4x²−4x+1≥0 Δ=0,

	4		1
x0=		=
	2*4		2

	1
4x2−4x+1≥0 ⇔ 4(x−		)2≥0 → parabola z ramionami w górę
	2

Szkic Odp. Rozwiązaniem nierówności 4x²−4x+1≥0 jest x∊R, czyli każda liczba x spełnia tę nierówność 2) 4x²−4x+1>0

	1
Odp. Rozwiązaniem nierówności 4x2−4x+1>0 jest x∊R \ {		}
	2

lub możesz też zapisać odpowiedź w sposób następujący:

	1		1
x∊(−∞,		) ∪ (		,+∞)
	2		2

3) 4x²−4x+1≤0

	1
Tylko x=		spełnia nierówność
	2

	1
Odp. Rozwiązaniem nierówności 4x2−4x+1≤0 jest x=
	2

4) 4x²−4x+1<0 Nierówność sprzeczna Odp. Nierówność 4x²−4x+1<0 nie ma rozwiązań

maciu: nie nie chodziło mi o to wiem ze jak ujemna to sprzeczna,chodzi o to ze dalej delta 0 (czyli 1 miejsce zerowe) tak jak w komentarzu 19 22,tylko że ramiona inaczej skierowane o to mi chodzi i opisac mi wszystkie tez schematy wtedy jakie były o to mi chodzi

maciu: dzięki yht

maciu: a czy jak napisze słownie tylko x=4 spełnia nierównośc to zaliczą? czy trzeba x( itp...

yht: Słownie tylko x=4 spełnia nierówność jeśli tak napiszesz to zaliczą

maciu: każdemu dziękuje,naprawde szczerze kto mi pomagał i pomaga bez względu na to czy zdam czy nie ,naprawde wam dziękuje

yht: maciu, polecam Ci zająć się tym 5/ −tym przykładem od Ety − on jest nietypowy a takie też mogą dać (dla zmyłki...)

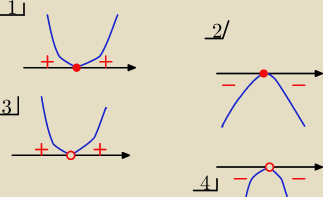
Eta: 2 przypadek gdy Δ=0 ( parabola do tyka osi w jednym punkcie w miejscu zerowym , które liczysz

	−b
ze wzoru x1=		/
	2a

1/ i 3/ Δ=0 i parabola ramionami do góry to nierówność o znaku ≥0 wtedy x∊R o znaku >0 wtedy x∊R\ { x₁} ( bez miejsca zerowego) o znaku <0 −−− sprzeczna ) z rys 3/ ( bo paraboli nie ma pod osią o znaku ≤0 −−−− tu parabola dotyka osi i nie ma jej pod osią wtedy : x= x₁ −−−− tylko jeden punkt Podaj teraz Ty podobnie to co ja napisałam ale dla rysunków 2/ i 4/

maciu: wezme sie za ten przyklad

maciu: 5 przyklad nie wiem gdzie blad 3x−(x+1)²<=5x−x² 3x−x²+2x+1<=5x−x² 5x−x²+1<=5x−x²

Eta: I został 3 przypadek gdy Δ>0 czyli dwa miejsca zerowe ( a to już umiesz ! tylko pamiętaj kiedy przedziały ( ) a kiedy < >

maciu: 3 przypadek umiem dobrze

Eta: 3x−1( x²+2x+1) teraz opuszczając nawias zmieniasz wszystkie znaki w nawiasie na przeciwne 3x −x²−2x−1 np: − 2( x−1)² = −2( x²−2x+1) = teraz mnożysz każdy wyraz w nawiasie przez −2 podaj wynik np −3(x−2)² = .... podaj wynik

Eta: Przeanalizuj te 2 przypadki ( skoro trzeci umiesz)

maciu: tam nie powinno byc 3x + x² skoro zmienia sie znak na minus a tam jest przed tym jeszcze −1

yht: opuszczając nawias zmieniasz wszystkie znaki w nawiasie na przeciwne czyli (w nawiasie) był + przed x² to po opuszczeniu nawiasu będzie −x²

maciu: jeszcze raz te piate probuje 3x−(x+1)²<=5x−x² 3x−(x²+2x+1)<=5x−x² 3x zmieniam znaki +x²−2x−1<=5x−x² x+x²−1<= 5x−x² 2x²−4x−1<=0

maciu: pojmuje ale mnie myli bo tam przed nawiasem było −1 to mi koliduje

yht: w nawiasie było (x²+2x+1) ponieważ przed nawiasem jest minus −(x²+2x+1) to znaki zmieniam na przeciwne: −x²−2x−1 czyli ma być 3x −x²−2x−1 ≤ 5x−x²

yht: jeśli przed nawiasem jest −1 to opuszczając nawias też zmieniasz (wszystkie) znaki w nawiasie na przeciwne: −1(x²+2x+1) = −x²−2x−1 sytuacja z −1(x²+2x+1) jest dokładnie identyczna co sytuacja z samym minusem przed nawiasem: −(x²+2x+1)

maciu: to w której linijce jest blad w 22 18?

Eta: Specjalnie Ci napisałam −(......... ) to −1( ........) żebyś wiedział jak będzie np −3(..........)

maciu: czyli to czy −1 czy 1 przed nawiasem nie ma nic do rzeczy?

maciu: Eta daj jeszcze ze 2 przykłady podobne do 5

maciu: i raczej wydaje mi sie ze to jest rozkaz

Eta: Dokładnie tak

Eta: 6/ 2x² +1 > −2( x−3)² 7/ 2(x+1)² ≤ 5 −(x+3)²

maciu: a dajmy na to że taka sytuacja −2(−x²+x+3) to to samo jak pomnozyc to wszystko przez −2? a jeśli nic nie stoi przed nawiasem to co?

Eta: ..= 2x²−2x−6

maciu: to jest żałośnie proste

Eta: 2(−x²+2x−5) = ....

Eta: 5x + ( −x²+3x−8)=.....

maciu: a jakby było 2(−x²+x+3) to −2x² +2x+6 tak

Eta: właśnie tak!

maciu: no przecież ja to dawno wiedziałem

Eta:

maciu: 22 35 −5x²+15x−40

Eta: Źle ! jeszcze raz ...... popraw

Eta: 5x zostaw w spokoju ( bo tam nie ma mnożenia!

maciu: aha no tak ma być 5x+x²−3x+8

Eta: tak ! i jeszcze koniecznie zredukuj ( bo jak policzysz deltę ... dla czterech wyrazów? x²+2x+8 ( bo 5x −3x=....

maciu: to wiadomo przecież,wezme sie za te dwa przyklady 22 34 ,35, tylko musze okno dACHOWE ZAKLEIC

bezendu: Delta dla czterech wyrazów ? Δ²−6

Eta: A co? komary Ci wpadają?

Eta: bezendu .....to tłumaczenie "po maciowemu" ?

maciu: Nie bydlo sasiada caly czas szczeka

Eta: No to teraz zadanie bojowe rozwiąż nierówność: 2x² −(x−2)²≤ 3x+10

Eta: i taką: 3x² −2( x²+1) ≤ 4x−6

maciu: najpierw dwie poprzednie

Eta: Ok .... ja mam czas , ja poczekam

Metis: Skąd macie taką cierpliwość − podziwiam.

maciu: 3x²−2(x²+1)<=4x−6 3x²−2x²−2<=4x−6 x²−2<=4x−6 x²−4x+4<=0 6

maciu: ty mnie podziwiaj ,że mam taką cierpliwość żeby się cały dzień uczyć

Eta: Na razie ok teraz podaj rozwiązanie

maciu: 2x²−(x−2)²<=3x+10 2x²−(x²−4x+4)<=3x+10 2x² − x² +4x−4<=3x+10 x²+4x−4<=3x+10 x²+x−14<=0

maciu: źle ostatnie linie −x²+4x−4<= 3x+10 −x²+x−14

Eta: ok ale to jeszcze nie koniec ......... podaj rozwiązanie tej nierównosci

Eta: 23:12 było dobrze 23:17 źle

maciu: a jak by było 2x (x²+x+10)

maciu: a jak by było 3 (−x² +x + 2) ?

Eta: a*b=0 ⇔ a=0 lub b=0 2x( x²+x+10)=0 ⇔ 2x=0 lub x²+x+10=0 x=0 lub i delta : Δ= 1−40 = −39 <0 to brak następnych rozwiazań Odp: tylko x= 0 jest rozwiązaniem

Eta: 23:23 podaj sam ..... zobaczymy czy dobrze "główkujesz" ?

maciu: x=−2

maciu: −3x²+3x+6

maciu: mi sie wydaję że x−2 ma być

Eta: Pisz czy to równanie czy nierówność !

Eta: "mi si wydaje" ,że ..... Nic w matematyce nie może się "wydawać" ! Ma być konkretna odpowiedź!

maciu: a to jakas roznica?

maciu: powiedzmy że równanie

Eta: Szalona!

maciu: o boże

maciu: 3−(x²+x+1)=0 3−(x²+x+1)>0 czym to sie różni

maciu: −3x²−3x−3=0

Eta: 3(−x²+x+2)=0 /:3 −x²+x+2=0 i licz deltę i x₁ i x₂ −−−−−− i to będzie odpowiedź ( tylko dwie liczby) Natomiast 3( −x²+x+2) >0 /:3 −x²+x+2 >0 po wyliczeniu delty i miejsc zerowych rysujesz parabolę ramionami o dołu i podajesz przedział otwarty .......... Pisałeś,że to umiesz! Widzisz już "jaka różnica" ? między rozwiązaniem równania ? a rozwiązaniem nierówności ?

maciu: no to rozumiem,ale pytalem czy z nawiasami sie działa tak samo w równaniach i nierównosciach kw

Eta: Skąd wziąłeś to 3−(x²+x+1)=0 ( sam wymyśliłeś? Robisz taki mętlik, że już nie wiem o co pytasz? czy o : 3(−x²+x+1) =0 czy o : 3 −(−x²+x+1)=0

maciu: nie pomyliło mi sie miało być −3(x²+x+1) = 0 −3(x²+x+1) <0

Eta: W każdym równaniu i w każdej nierówności ..... "działasz" tak samo aż do uporządkowania i po przeniesieniu wszystkiego na lewą stronę! W równaniach : podajesz x= ...lub x=... jak istnieją ( czyli pojedyńcze liczby W nierównościach : rysujesz parabolę i podajesz przedziały o ile istnieją! T Tak mnie już wymęczyłeś ,że idę teraz na herbatkę !

maciu: pojmuje

Eta: I to jest pocieszajace wreszcie wszystkie słowa "nie pojmuję" zamieniasz na "pojmuję"

maciu: 22 02,te schematy na 100% są dobre i zawsze tak jest?

maciu: nie ma wyjątków wtedy? tak?

Eta: tak!

maciu: no cóż,nie pojmuje tego,ale naucze sie tego na pamiec

Eta: Byle było 30%

maciu: prosze 1 ostatnia nierownosc na koniec dnia

maciu: bardzo prosze

Eta: 1/ 2x²+6x > 3x²+4x 2/ 2( x²−2x) ≤ (x+3)(x−2) podaj kompletne rozwiązanie wraz z rysunkiem i Odp: .......

maciu: zad 1 (wpierw dane) 2x²+6x>3x²+4x −x²+2x>0 a=−1 b=2 c=0 później delta

Eta: Można bez delty No ale licz ... deltę

maciu: zaraz

maciu: zad 2 2(x²−2x)<=(x+3)(x−2) 2x²−4x<=x²−2x+3x−6 2x²−4x<=x²+x−6 x²−5x+6<=0

Eta: Na razie ok ale masz podać kompletne rozwiązanie z rysunkiem i odp

maciu: zaczne od zad nr 1

Eta: Ja czekam

maciu: zad 1 x(0,2)

Eta: ( jeszcze na rys . zaznacz kółeczka niezamalowane

maciu: wiem,ale nie umiem na klawiaturze

Eta: No to jeszcze czekam na to drugie .....

maciu: zad 2 x(2,3)

Eta: Jakie nawiasy? przy ≤0

Eta: Musisz na to zwracać uwagę !

maciu: <> ja wiem to dobrze,ale nie przywiązuje do tego większej wagi tym bardziej że pisze na klawiaturze,na maturze bede o tym pamietal

Metis: Jeśli nie pamiętasz o tym teraz, to na maturze nie będziesz tym bardziej

Eta:

maciu: ale ja pamiętam o tym teraz tylko co innego pisac na kartce,a co innego na tej klawiaturze bawic sie w te przedziały

Eta:

bezendu: Eta Ty masz anielska cierpliwość, ja Cię podziwiam

maciu: nie pisz głupstw,bo nie ja jedyny wrzucam zadania,wiele osób na tym forum ma większe braki niż ja i nikt się nie czepia(chodzi mi o poprawkowiczów) zrozumiano?

bezendu: Maciu nie podskakuj

maciu: nie podskakuje