pomocy nierówności historyk: mam problem z końcówką nierówności to znaczy np ; a)x²−7x−8>0 wypisuje a b c licze delte miejsca zerowe x1 x2 i potem trzeba narysowac parabole zaznaczyc na osi x zaden problem ale kiedy mam napisac jakie nawiasy cxy okragle czy ostre to juz jest problem ten przykład jest prosty ale co kiedy np b delta wyjdzie 0 liczbe x0 wyjdzie np 4 a znak przy nierownosci jest ≤0 jaki wtedy jest przedzial zawsze mi sie to myli kiedy zbior pusty kiedy nalezy do liczb rzeczywistych itd najprosciej jest kiedy mam dwa miejsca zerowe

6latek : jak masz zwrot > lub < to przedzial otwarty czyli x∊(.....) jak maz zwrot ≤ lub ≥ to przedzial zamnkiety czyli x∊<.....>

historyk: okej to wtedy kiedy mam dwa miejsca zerowe może dam ci przykład na przykładzie podobno się lepiej tłumaczy a) x²+8x+16≤0 Δ=0 x0=4 i co teraz

historyk: sory −4

Jerzy: Jakie wartości przyjmuje funkcja: f(x) = x² + 8x + 16 ?

historyk: wiem , że są jakieś prace na serwerze ale czy jest szansa na dokończenie tłumaczenia ? bardzo proszę

historyk: jakie wartości ?

Jerzy: No właśnie ...jakie ? ...potrafisz naszkicować wykres tej funkcji ?

historyk: dodatnie bo wspólczynnik a jest dodatni dlatego ramiona paraboli tej nierównosci będą skierowane do góry zaznaczam na osi x −4 chodzi mi o zbiór xe

historyk: ≤ i są minusy więc nie ma na paraboli minusów dlatego zbiór pusty

Jerzy: Przyjmyje tylko wartości nieujemne ( czyli dodatnie lub zero ). Masz nierówność: x² + 8x + 16 ≤ 0 , zatem kiedy ona jest spełniona ?

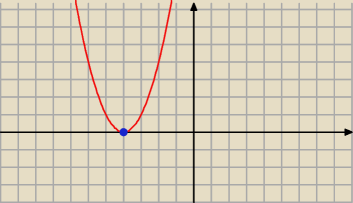
5-latek: ta nierownosc x²+8x+16≥0 jest spelniona tylko dla x=−4 Masz nierownosc slaba ≤ Zobacz ze wartosci tej funkcji sa nieujemne tzn rowne 0 lub dodatnie ta parabola dotyka osi oX w punkcie x=−4 i wtedy wartosc tej funcji y=0 i ramiona paraboli wzosza sie and os OX czyli wartosci funkcji sa dodatnie TY w swoje nierownosci masz ≤0 czyli masz miec wartosci ujemne co nie zajdzie bo widzac na wykresie bad rowne 0 czyli dla x=−4 Rozwiazaniem tej nierownosci jest x=−4 (pomono se to jest nirownosc Inaczej byloby gdyby to byla nierownosc ostra czyli taka <0 Wtedy nie ma rozwiania bo nie ma takiego x_xa dla ktorego wartosc tej funkcji jest ujemna (wyres nielezy pod osia OX

5-latek: WItaj Jerzy A ja sie tyle opisalem

Jerzy: Witaj

historyk: Jerzy ta parabola pokazuje tylko wartości dodatnie a mam ≤ czyli muszą byc ujemne ale nie ma więc czy zbiór jest pusty ?

historyk: 5−latek dzięki za tyle pisania i rysunek

5-latek: Piszse jedna reka bo lewa mam uszkodzona (miala bliskie spotaknie z siekiera )

Jerzy: A czy ta funkcja przyjmuje wartość 0 ?

historyk: 5−latek współczuje Jerzy : −4 i chyba zero też

Jerzy: Jakie − 4 ? ..... patrz na wykres ...jaka jest najmniejsza wartość tej funkcji ?

5-latek: Wies zhistoryk −dobrze ze nie sciegna tylko miesnie poprzecinane pod kciukien i bylo szyte .

historyk: dużo zdrowia życzę 5 latek tymaczasem Jerzy najmniejsza wartosc do 0 ?

5-latek: nalezy historyk napisac tak dla x=−4 funkcja ta przyjmuje wartosc y=0 zobacz na rysunku bo co to znaczy −4 i chyba zero tez ?

5-latek: Dziekuje

historyk: no lepiej o wiele lepiej brzmi x=−4 y=0

historyk: i jak to już wiem to jak odczytac przedział

5-latek: w tej konkretnej nierownosci nie bedzie przedzialu jrdynym rozwiazaniem tej nirownosci jest x=−4 =========================================

historyk: to jak to zapisac x∊ w klamerce −4

5-latek: mozesz zapisac tak x=−4 lub x∊{−4}

5-latek: taki zapis oznacza zbior jednoelementowy

Jerzy: x² + 8x +16 ≤ 0 ⇔ x = −4 lub inaczej : x ∊ {−4}

historyk: dobrze bo np gdyby była taka sytuacja ≥ to są plusy wtedy

Jerzy: wtedy: x ∊ R ( każda liczba spełnia nierówność )

5-latek: Jerzy bedzie Ci pomagal

historyk: a kiedy pisze się ze x∊r/i tu liczba

Jerzy: a co to jest r ?

historyk: liczby rzeczywiste dobrze 5−latek oszczędzaj rękę

Jerzy: x² + 8x + 16 > 0 ⇔ x ∊ R/{−4}

historyk: a to samo jest tylko ze bez R ale to samo okej a kiedy jest zbiór pusty

Jerzy: x² + 8x +16 < 0 ( brak rozwiązań )

historyk: to wszystko zalezy od ≤ ≥ czy < >

Jerzy: Tak

historyk: a np mam x² +4>0 Δ=−16 nie ma miejsc zerowych to rysuje os x ale parabola jest w powietrzu ramiona skierowane w dół plusy bo >

historyk: znaczy do góry sorki

Jerzy: a dlaczego w dół ? x² + 4 > 0 jest spełnione dla dowolnego x

historyk: poprawiłam 11 54 do góry a dodatnie

historyk: jaki będzie tutaj przedział

Jerzy: x ∊ R ..patrz 11:54

historyk: okej a gdyby było < to są minusy

Jerzy: x² + 4 < 0 ⇔ x∊ {Φ} ( brak rozwiązań )

historyk: czyli jak mam inny przykład −x²−1<0 Δ=−4 nie ma ms zerowych rysuje os x parabola w powietrzu tylko ze ramiona w dół

Jerzy: ta parabola leży całkowicie pod osią OX, a więc ta funkcja przyjmuje tylko wartośći ujemne, zatem: −x² −1 < 0 ⇔ x ∊ R

historyk: myslę , że już coś kumam dzięki Jerzy a mam takie pytanie podchodzę do matury poprawkowej w sierpniu czy są jakieś zadania które warto powtórzyc mam równy tydzień na powtórkę