liczny zespolone dag: Znaleźć wszystkie liczby zespolone z takie, że z⁵ = −32i.

jc: z = −2i (cos 2kπ/5 + i sin 2kπ/5), k = 0,1,2,3,4

6latek: z=⁵√−32i r=|z|=√0²+(−32)²= 32

	3
φ=		π
	2

	3/2π+2*0*π		3/2π+2*0*π
ω0=5√32(cos		+isin		)=2(cos54o+isin54o)
	5		5

=================

	3/2π+2*1π		3/2π+2*1*π
ω1= 2(cos		+isin		=
	5		5

	7		7
2(cos		π+isin		π)=2(cos126o+isin126*o)=
	10		10

=2(−cos54^o+isin54^o ) ===================

	11		11
ω2= 2(cos		π+isin		π)= 2(cos198o+isin198o)= 2(−cos18o−isin18o)
	10		10

=====================

	15		15
ω3= 2(cos		π+isin		π)= 2(cos 270o+isin270)= 2(0+1i)=2i
	10		10

===========

	19		19
ω4=2(cos		π+isin		π)= 2(cos342o+isin342o)= 2(cos18o−isin18o)
	10		10

=================

jc: @6latku, Twoje rozwiązanie jest dobre dla komputera. Spróbuj zapisać wynik nie używając sinusa i kosinusa.

6latek: Witaj Liczylem to wedlug wzoru . Wzorowalem sie tez na na kursie . Tylko on tam podaje kąty gdzie idzie ladnie nawet zapamietac bo 30,45,60,90 i 0 To w takim razie musialbym z tablic albo na kalkulatorze odczytac te kąty . czy tu chodzi o co innego ?

jc: Dla komputera sposów w sam raz. Natomiast dla nas czytelniejszy jest na ogół zapis pierwiastek = (jeden z pierwiastków)*(pierwiastek n−tego stopnia z 1)^k Np. z² = −9, z = ± 3 3 = jeden z pierwiastków z 9 ± 1 = dwa pierwiastki z jedynki

jc: Miało być z² = 9

6latek: Ja sobie jeszcze raz przypomne to jak on to robil ale przypominam sobie ze robil ze wzoru

	2π		2π
ωk=ωk−1(cos		+isin		)
	n		n

	2
Ale tutaj tez to nie bedzie takie proste bo mamy cos		π= 72stopnie
	5

Wezmy np pierwiastek stopnia 5 z jedynki to jest naprawde w cholere liczenia bo wychodzi ze musimy rozwiazac rownanie z⁵−1=0 (z−1)(z⁴+z³+z²+z+1)=0 z−1=0 z=1 teraz nie jest on pierwiastkiem pierwotnym bo z=1 jest pierwiastkiem stopnia czwartegi z jeden (nie wiem czy to ma tutaj jakies znaczenie rozwiazujac rownanie z⁴+z³+z²+z+1=0 (tutaj bedzie duzo liczenia dostaniemy

	−1−√5+i√10±2√5
z1,2=		}
	4

	−1+√5±i√10±2√5
z3,4=		}
	4

6latek: Moze ktos pokazac jak policzyc pierwszse dwa pierwiastki wedlug tego sposbu co napisal jc

jc: @6latku, gratuluję rozwiązania równania z⁵ = 1. O jakie dwa pierwsze pierwiastki pytasz?

Mila: (−2i)⁵=−32i ( liczysz w pamięci) Potem wzór jak kolega JC.

bezendu: Polecam mój wpis https://matematykaszkolna.pl/forum/263521.html 31 październik 21:52

6latek: dziekuje za wpisy Wroce do tego po poludniu po pracy jc te ω₀ i ω₁

jc: @6latku, zⁿ = w = r ( cos α + i sin α) Twoje tozwiązanie z = r^1/n [ cos (α+2kπ)/n + i sin (α+2kπ)/n ] Moje rozwiązanie z = u (cos 2kπ/n + i sin 2kπ/n), gdzie u jest jednym z pierwiastkow równania uⁿ = w. k = 0,1,2,3,...,n−1 Jeden z pierwiastków równania z⁵ = −32 i jest oczywisty. Jest to liczba −2i. arg(−2i) = −90^o Argumenty u mnie: −90 = 270 −90 + 72 = −18 = 342 −90 + 2*72 = 54 −90 + 3*72 = 126 −90 + 4*72 = 198 Argumenty u Ciebie (te same liczby, ale w innej kolejności) 270/5 = 54 54 + 72 = 126 54 + 2*72 = 198 54 + 3*72 = 270 54 + 4*72 = 342 −−−−−− Spróbuj rozwiązać po swojemu równanie z⁴ = (3+4i)⁴. Zobaczysz o co chodzi.

6latek: Mozna to rozwaizac tak Mamy juz jeden pierwiastek ω₀=3+4i

	2π		1		1
ω1= (3+4i)*(cos		+isinU{2π}=(3+4i)*(cos		π+isin		π)=
	4		2		2

3*cos0,5π+3isin0,5π+4icos0,5π+4i²sin0,5π= 3*0+3i*1+4i*0−4= 3i−4=−4+3i ω₂= (3i−4)*(cos0,5π+isin0,5π)= 3i*cos0,5π+3i²sin0,5π−4*cos0,5π−4isin0,5π= 3*0−3−0−4i=−3−4i ω₃= (−3−4i)(cos0,5π+isin0,5π)= −3*cos0,5π−3isin0,5π−4icos0,5π−4i²sin0,5π= −3i+4 Bedziemy mieli takie pierwiastki ω₀= 3+4i ω₁= −4+3i ω₂= −3−4i ω₃= 4−3i jc to bylo w sumie proste Teraz Cie zapytam wlasnie o to co pisalem wczesniej Mamy tak np z⁵= 3+4i⁵ z=⁵√(3+4i)⁵ zewzoru ⁿ√xⁿ=x mamy jeden pierwiastek czyli ω₀=3+4i

	2π		2π
licze ω1= (3+4i)*(cos		+isin		)
	5		5

	2π
Teraz jak policzyc dalej bo		= 72o a to juz taka ladna (tzn kazda liczba jest
	5

ladna ale do policzenia juz nie taka ladna

Mila: z⁴ − (3+4i)⁴=0 [z²−(3+4i)²]*[z²+(3+4i)²]=0⇔ [z²−(3+4i)²]=0 lub [z²+(3+4i)²]=0 (z−(3+4i))=0 lub (z+(3+4i))=0 lub [z²−(3+4i)²*i²]=0⇔(z−i(3+4i))=0 lub z+i(3+4i)=0 z=3+4i lub z=−3−4i lub z=i*(3+4i) lub z=−i(3+4i) z=3+4i lub z=−3−4i lub z=−4+3i lub z=4−3i

6latek: Dobry wieczorMilu Pozdrawiam

	2π
A co zrobic jak bedzie np ten kąt		?
	5

Co podsatwic za cos i sin ?

Mila: Trzeba policzyć. Kilka razy liczyłam na forum.

Mila: Witam ciepło.

jc: @6latku. Rozumiem, że można zamienić + na − lub odwrotnie, pomylić litery, ale opuścić nawias? z⁵= 3+4i⁵ ? z⁵ = 1, z = 1 lub z⁴+z³ +z +1 = 0 Wydawalo mi się, że wiesz, jak to policzyć (3.07 17:03). Na równania z⁴ + a z³ + b z² + az +1 = 0 jest taki sposób: dzielimy równanie przez z², wprowadzamy nową zmienną w = z + 1/z, znajdujemy w, a potem znajdujemy z. Spróbuj Zauważ, że z + 1/z = 2 cos α, gdzie α = 72^o (rozwiązanie dodatnie) lub α=144^o (rozwiązanie ujemne). Sinusy możesz potem znaleźć w zwykły sposób.

6latek: jc ale ja je tak rozwiazywalem

	1
t=1+
	z

	1
z2+		= t2−2
	z2

Dostaniemy rownaie t²+t−1=0

	−1−√5
t1=
	2

	−1+√5
t2=
	2

Pozniej wracamy do podstawienia Dostajemy dwa rownania kwadratowe do rozwiazania i dostajemy rozwiazania 3.07 17:03

	1
Powiem tak . Nie znam na tyle dobrze liczb zespolonych zeby wiedziec ze z+		=2cosα
	z

Racje mial PW ze liczb zespolonych nalezy uczyc sie dwa lata a nie dwa miesiace(a juz nie kilka dni tak jak ja . Ale moge np policzyc sin18^o bo np wiem ze bok 10 kata foremnego wpisanego w okrag o r=1 ma dlugosc

√5−1
	=a10
2

	π		a10		√5−1
sin		=18o=sin		=		=cos72o
	10		2		4

sin72^o=√1−cos²72=

	√5−1		5−2√5+1		4−2√5		2−√5
cos272= (		)2=		=		=U{2(2−√5){16}}=
	4		16		16		8

6latek: Za szybko wyslalem

	2−√5		8−(2−√5)		6+√5
1−		=		=
	8		8		8

	6+√5
wiec sin72o=√
	8

Liczenie teraz np na klasowce tego to obled . No chyba ze tutaj chodzi o co innego

jc: Równanie z⁴ + z³ + z² + z +1 = 0 daje nam różne od 1 rozwiązania równania z⁵ = 1. Dlatego |z| = 1, z = cos α + i sin α, α = 72, 2*72, 3*72, 4*72. Jeśli z = cos α + i sin α, to 1/z = cos α − i sin α, i dalej z + 1/z = 2 cos α. Zrób koniecznie rysunek, zobaczysz dalczego tak jest Nie uważam, żeby 2 lata na liczby zespolone były konieczne. Są trudniejsze rzeczy, jak indukcja, granica, ...

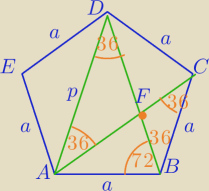
Mila: ΔADF∼ΔBCF |DF|=a

p		a
	=
a		p−a

p*(p−a)=a² p²−a*p−a²=0 Δ=a²+4a²=5a²

	a−a√5		a+a√5
p=		<0 lub p=
	2		2

	a*(1+√5)
p=
	2

	1   a 2		√5−1
cos(72o)==		=
	a*(1+√5)   2		4

	√5−1
sin(18o)=
	4

	0.5p		1+√5
cos(36o)=		=
	a		4