zespolone kyrtap: z⁶ = −64 z = ⁶√−64 IzI = √64² = 64

	64
cosα =		= 1
	64

sinα = 0 α = 0

	0+2π		0+2π		1		√3
w0 = 2( cos		+ isin		) = 2(		+		) = 1 + √3 dobrze
	6		6		2		2

wyliczony pierwszy pierwiastek ?

Janek191: cos α = − 1 !

kyrtap: o ja

kyrtap: liczę od nowa ale cała procedura dobrze tak?

Janek191:

kyrtap: czy ten uśmiech mówi że tak?

kyrtap: czyli w₀ = √3 + i

kyrtap: dziwnie mi wychodzi z tymi pierwiastkami

kyrtap: jeżeli w₁ = 2 to chyba coś nie tak prawda

kyrtap: ktoś zweryfikuje to?

Mały Książę: masz rację, jest błąd

Mały Książę: ja się nie znam na matematycę przyszłem popatrzeć tylko niestety

kyrtap: dobra zapomniałem " i " teraz pasi

Mila: z⁶=−64 z=√−64 |z|=64 ( −64 to liczba rzeczywista, gdzie leży?) φ=π

	π+2kπ		π+2kπ
z=6√64}*(cos		+i sin		)
	6		6

	π		π
z0=6√64*(cos(		)+i sin(		))
	6		6

	√3		1
z0=2*(		+		i )=√3+i
	2		2

	3π		3π		π		π
z1=2*(cos		+i sin		)=2*(cos		+i sin		)=2*(0+i*1)=2i
	6		6		2		2

Licz dalej

kyrtap: wyliczyłem ale trapi mnie to że metodą szybszą błędnie wyliczyłem chodzi mi o to że mogę domyślić się 2 pierwiastków a mianowicie 2i oraz −2i potem i potem liczę pozostałe pierwiastki

bezendu: Wiesz co to jest sześciokąt foremny ? Koło trygonometryczne? W takich zadaniach to jest niezbędne. Na kolosie nie zdążysz zrobić wszystkich zadań bez tej wiedzy.

kyrtap: na czym polega koło trygonometryczne?

kyrtap: przy 8 pierwiastkach naprawdę wychodzi dużo liczenia

bezendu:

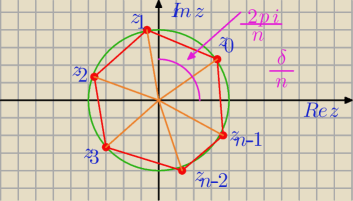
	δ		δ
Jeden z pierwiastków tego wielokąta jest w punkcie zo=n√r(cos		+sin		) a kąty
	n		n

	2π
pomiędzy promieniami wodzącymi sąsiednich wierzchołków są równe
	n

Zbiór pierwiastków stopnia n≥3 z liczby zespolonej pokrywa się ze zbiorem wierzchołków n−kąta formenego.

bezendu: Koło trygonometryczne to akurat dla argumentu. Dla pierwiastków stopnia n≥3 korzystamy z n−kata formnego. pierwiastek stopnia 3 trójkąt rówwnoboczny pierwiastek stopnia 4 kwadrat pierwiastek stopnia 5 pięciokąt foremny itd itp

Mila: Obejrzę "Różyczkę", to wyjaśnię szybszą metodę.

kyrtap: ale to i tak nie zmienia faktu bezendu że muszę korzystać ze wzoru

bezendu: Ale nie 8 razy ! Ciekawe jak będziesz mieć pierwiastek stopnia 12. To co 12 razy pod wzór ?

kyrtap: no to jak podaj twój sposób na jakimś prostym przykładzie bo nie czaję

bezendu: Za dużo pisania, sam spróbuj zrobić, proste zadanie na początek Oblicz ³√−27 Korzystasz z tego co podałem 21:52. za n podstawiasz 3 i masz trójkąt równoboczny

kyrtap: mam kąty po 120 stop

kyrtap: promień wodzący r = 27

kyrtap: z₀ = 3( cos120 + isin120) tak?

bezendu: Źle. I na studiach piszemy w radianach a nie stopniach. Ja już uciekam, Mila Ci wyjaśni lepiej ode mnie.

kyrtap: czekam na Milę mam nadzieję że 2 sposoby będę umiał

Gray: Zobacz na str. 12. Dobrze to wytłumaczono http://home.agh.edu.pl/~gora/algebra/Wyklad02.pdf

kyrtap: też trzeba trochę liczyć i tak

Mila: z=⁶√−64 |−64|=64 z₀=2i sprawdzam, (2i)⁶=2⁶*(i²)³=−64

	2kπ		2kπ
zk=2i*(cos		+i sin		), k∊{1,2,3,4,5}
	6		6

No to liczymy:

	2π		2π		1		√3
z1=2i*(cos		+i sin		)=2i*(		+i*		)=−√3+i
	6		6		2		2

4π

4π

2π

2π

1

√3

z2=2i*(cos

+i sin

)=2i*(cos

+i sin

)=2i*(−

+i

)⇔

6

6

3

3

2

2

z₂=−√3−i z₃=2i*(cosπ+i sinπ)=2i*(−1+i*0)=−2i z₄= z₅=

Mila: ?

kyrtap: ok dzięki

Mila: Policz do końca, jak widzisz tu nie szukasz φ.

kyrtap:

	8π		8π		4		4
z4 = 2i * (cos		+ i sin		) = = 2i (cos		π + i sin		π) = 2i (cos(π +
	6		6		3		3

	π		π		1		√3
		) + i sin(π +		)) = 2 i (−		+ i (−		)) = −1 − √3
	3		3		2		2

kyrtap: chyba ten sposób będzie dobry dla mnie